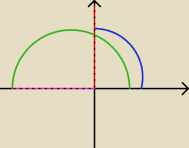
 1. π2<arg(−z)<π
Narysowałem tak jak na górze, nie wiem co zrobić z tym arg(−z) jak jest arg(z) to wiem co robić
ale nie wiem jak to wygląda przy innych arg
1. π2<arg(−z)<π
Narysowałem tak jak na górze, nie wiem co zrobić z tym arg(−z) jak jest arg(z) to wiem co robić
ale nie wiem jak to wygląda przy innych arg
| π | ||
Rozwiązaniem nierówności | <arg z<π jest część płaszczyzny, w której leżą punkty (x,y) | |
| 2 |
| π | ||
Żeby dostać | <arg(−z)<π wystarczy ten obszar odbić symetrycznie względem początku układu | |
| 2 |
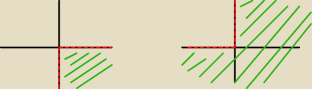 Czyli dla arg(−z) to będzie ten 1 wykres ? czy ten 2 ? czy jeszcze źle rozumiem
Czyli dla arg(−z) to będzie ten 1 wykres ? czy ten 2 ? czy jeszcze źle rozumiem
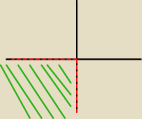 to zakładając że byłby przykład taki sam tylko zamiast arg(−z) to arg(sprzężenie z) to wykres
wyglądał by tak ?
to zakładając że byłby przykład taki sam tylko zamiast arg(−z) to arg(sprzężenie z) to wykres
wyglądał by tak ?
