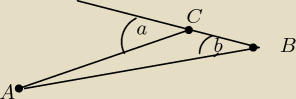
z arkusza D.: Wykaż, że jeśli a=2b to trójkąt ABC jest równoramienny. Kompletnie nie wiem od czego zacząć− wytłumaczycie?

Basia: ∡ACB = 180−α=180−2β ⇒ ∡BAC = 180−∡ABC−∡ACB = 180−β−(180−2β) = 180−β−180+2β=β stąd: ∡BAC = ∡ABC = β ⇒ △ACB=△ABC jest równoramienny

D.: mam pytanie: skąd się wzięło 180?

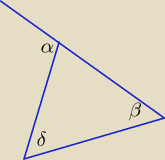
Bogdan: albo: α = β + δ i α = 2β ⇒ 2β = β + δ ⇒ β = δ

D.: hmmm... może to drugie to nawet prostsze jest...

Basia: które 180 ? α+ACB=180 bo α o ACB to kąty przyległe(to pierwsze 180) suma kątów w każdym trójkącie wynosi 180 (to drugie 180) a wiesz jakim twierdzeniem Bogdan się posłużył ? jak nie wiesz to pytaj

D:: ostatecznie i tak zapisałam w swoim zeszycie twoje rozwiązanie, ale fakt− z tym 180 to już jest dla mnie oczywiste. Dzięki!