dowód z liczbami rzeczywistymi Ferie2k16: Udowodnij, że suma kwadratów trzech koljenych liczb naturalnych nie moze byc kwadratem liczby naturalnej. Doszedłem z sumą kwadratów do takiej postaci: 3(n² + 2n +1) + 2 i nie wiem jak wykazać, że to nie moze byc kwadrat liczby naturalnej. Dzięki za pomoc.

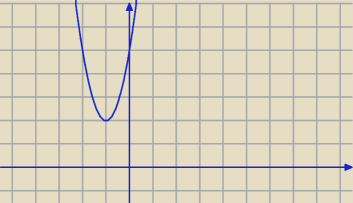
Jack: 3(n² + 2n + 1) + 2 = 3n² + 6n + 3 +2=3n² + 6n + 5 jesli dobrze policzyles... wtedy Δ < 0 a więc (patrz rysunek) nie ma miejsca zerowego, czyli nie ma takiej liczby ktora podniesiona do kwadratu dawalaby twoja liczbe... chyba

Ferie2k16: ktos potiwerdza?

Mila: Kwadrat liczby naturalnej przy dzieleniu przez 3 daje resztę 0 lub 1. n²+(n+1)²+(n+2)²=3n²+6n+5=3n²+6n+3+2=3*(n²+2n+1)+2 Liczba : 3*(n²+2n+1)+2 nie może być kwadratem liczby naturalnej ponieważ reszta z dzielenia przez 3 jest równa 2.

Jack: aaaaaaaaaaaa

Ferie2k16: A skad wiadomo, ze kwadrat liczby naturalneej przy dzieleniu przez 3 daje reszte 0 lub 1?