| 1 | ||
√x2−4 > | ||
| 2 |
| 1 | ||
x2−4> | ||
| 4 |
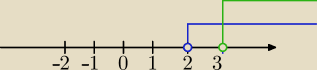 a) x−2>0 i log(x−2)>0
x>2 i log(x−2)>log1
x>2 i x>3⇔
x>3
D=(3,∞)
a) x−2>0 i log(x−2)>0
x>2 i log(x−2)>log1
x>2 i x>3⇔
x>3
D=(3,∞)

 b)
x2 − 4 ≥ 0 i 2√x2−4−1>0⇔2√x2−4>1 /2
b)
x2 − 4 ≥ 0 i 2√x2−4−1>0⇔2√x2−4>1 /2
| 1 | ||
(x−2)(x+2)≥0 i 4(x2−4)>1⇔x2−4> | ||
| 4 |
| √17 | √17 | |||
[x ∊ (−∞;−2> ∪ <2;∞) ] i (x− | )* (x− | )>0 | ||
| 2 | 2 |
| √17 | √17 | |||
[x ∊ (−∞;−2> ∪ <2;∞) ] i [x<− | lub x> | ] | ||
| 2 | 2 |
| √17 | √17 | |||
D=(−∞,− | )∪ ( | ,∞) | ||
| 2 | 2 |