Geometria Analityczna
bartek: 1. Dane są wierzchołki trójkąta : A=(2,2) B=(7,7) C=(10,3).Wyznacz długość trójkąta ABC
opuszczonej z punktu C.
2. Punkt C=(1,−3) jest wierzchołkiem trójkąta równobocznego ABC.Wyznacz współrzędne pozostałych
wierzchołków trójkąta, wiedząc, ze należna one do prostej o równaniu y=−x−+4.
16 gru 22:12
kaz: 1)
wyznacz pr.AB,potem pr.prostopadłą do niej przechodzącą przez C,a następnie rozwiąż układ
równań z tymi prostymi.Otrzymasz punkt na boku IABI,na który opuszczona jest
wysokość.Odległość tego punktu od C(10,3) będzie dł.wysokości.
16 gru 22:25
bartek: @kaz jeśli możesz to policzyć bo mi za żadne skarby nie może wyjść wyszło mi coś takiego:
pr.AB y=x pr.prostopadła y=−1x a nie wiem jak zaznaczyć, żeby przechodziła przez punkt C
16 gru 22:55
Godzio:
AB:
2=2a + b
7=7a+b −
−−−−−−−−−−−−−
−5 = −5a
a=1
b=0
y=x
prostopadła :
3= −1*10 +b
3=−10+b
b=13
y=−x+13
16 gru 23:08
Godzio:
teraz szukamy punktu wspólnego obu prostych
y=x
y=−x+13 => x=−x+13 => 2x=13 =>x =6,5 y =6,5
D(6,5 ; 6,5)
| | 7√2 | |
h=|CD| = √(6,5−10)2 + (3−6,5)2 = √12,25+ 12,25 = √24,5 = |
| |
| | 2 | |
16 gru 23:12
bartek: Dzięki jeśli można to prosiłbym tez o 2 zadanie
16 gru 23:17
Godzio:
już pomagam
16 gru 23:20
Godzio: bartek napisz jeszcze dokładnie to równanie ma być +4 czy −4
16 gru 23:22
bartek: y=−x+4 przepraszam za błąd
16 gru 23:28
Godzio:
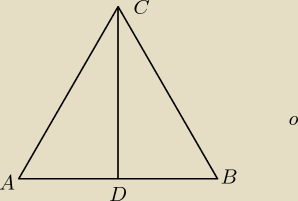
wiedząc że jest to trójkąt równoboczny :
AD = DB
AB=BC=CA
y
AB=−x+4
prosta przechodząca przez CD jest prostopadła do prostej y
AB czyli
y
CD = ax+b
−3 = 1*1 +b
−3=1+b
b=−4
y
CD = x−4
współrzędne punktu D to punkt przecięcia się prostych y
AB i y
CD
y
AB=y
CD
−x+4 = x−4
−2x=−8
x=4 => y=0
D(4,0)
długość CD:
|CD| =
√(4−1)2 + (0+3)2 =
√18=3
√2
2
√6 = AB => DB=DA =
√6
√6 = DB
√6 =
√ (xB−4)2 + (yB−0)2 podstwiam y
AB=−x+4
√6 =
√ (xB−4)2 + (4−xB)2 /
2
6 = 2x
B2 −16x
B +32
0=2x
B2 − 16x
B+26
0=x
B2 − 8x
B +13
i tutaj nie jestem pewien czy napewno tak ma być

bo wyniki takie średnie wychodzą
może ktoś sprawdzić czy poprawnie robiłem ?
17 gru 00:00
Godzio: ja już ide spać także jak coś to ktoś inny Ci pomoże

dobranoc wszystkim

17 gru 00:05
ANNA: Wszystko się zgadza. Po rozwiązaniu ostatniego równania kwadratowego otrzymujemy:
xB = 4+√3 ⇒ yB = −4−√3+4 = −√3
lub xB = 4−√3 ⇒ yB = −4+√3+4 = √3
Zatem pozostałe wierzchołki trójkąta mają współrzędne: (4+√3; −√3) i (4−√3; √3).
17 gru 00:30
kaz: wydaje mi się,że to poprawne rozwiązanie
17 gru 00:33
Bogdan:
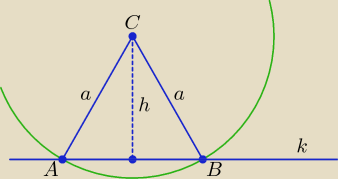
Zadanie jest dobrze rozwiązane, przedstawiam inny sposób rozwiązania tego zadania.
k: y = −x + 4 ⇒ x + y − 4 = 0
C = (1, −3)
| | |1*1 − 3*1 − 4| | | 1 | |
h = |
| = 3√2, 3√2 = |
| a√3 ⇒ a = 2√6 |
| | √1 + 1 | | 2 | |
Tworzymy okrąg o środku C i promieniu a: (x − 1)
2 + (y + 3)
2 = 24
Dla wyznaczenia punktów A i B rozwiązujemy układ równań:
1. (x − 1)
2 + (y + 3)
2 = 24
2. y = −x + 4
1. (x − 1)
2 + (−x + 7)
2 = 24 ⇒ x
2 − 8x + 13 = 0
x = 4 −
√3 i y =
√3
lub
x = 4 +
√3 i y = −
√3
Odp.: A = (4 −
√3,
√3), B = (4 +
√3, −
√3)
17 gru 00:59
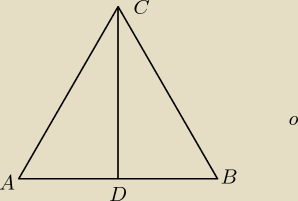 wiedząc że jest to trójkąt równoboczny :
AD = DB
AB=BC=CA
wiedząc że jest to trójkąt równoboczny :
AD = DB
AB=BC=CA
 bo wyniki takie średnie wychodzą
może ktoś sprawdzić czy poprawnie robiłem ?
bo wyniki takie średnie wychodzą
może ktoś sprawdzić czy poprawnie robiłem ?
 dobranoc wszystkim
dobranoc wszystkim 
 Zadanie jest dobrze rozwiązane, przedstawiam inny sposób rozwiązania tego zadania.
k: y = −x + 4 ⇒ x + y − 4 = 0
C = (1, −3)
Zadanie jest dobrze rozwiązane, przedstawiam inny sposób rozwiązania tego zadania.
k: y = −x + 4 ⇒ x + y − 4 = 0
C = (1, −3)