Długość dłuższego boku GIGANT: W równoległoboku dluższa przekątna ma długość 7 cm, kąt rozwarty wynosi 120*. kąt między dłuższym ramieniem równoległoboku, a jego przekątną ma miare 15*. Oblicz długość dłuższego boku. Mógłby mi ktoś wytłumaczyć jak zabierać się za tego typu zadania? Widziałem analogiczne zadania, często korzysta się z twierdzenia cosinusów. Tutaj nie widzę jak można go zastosować... Gdybym miał np. informację, że krótszy bok tego równoległoboku jest o połowę krótszy od dłuższego to bym zapisał to : 7² = x² + (¹₂)² + 2 * x * ^x₂ * cos 120* i dalej sprawa byłaby jasna, ale takiej informacji nie mam i nie wiem co zrobić... kompletnie nie mam pomysłu, help!

GIGANT: Tam oczywiście zamiast ¹₂ powinno być ^x₂ ...

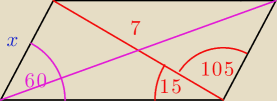
Jack: rysunek najwazniejsz... twierdzenie sinusow...

7		x
	=
sin 60		sin 15

Jack:

	√3
sin 60 =
	2

sin 15 = sin(45−30) w tablicach masz wzor na sin(alfa − beta) albo z cos (90 − alfa) = sin alfa, wiec cos 75 = sin 15 cos 2alfa = cos² alfa − sin ²alfa = 2cos²alfa − 1 cos 150 = 2cos² 75 − 1

	√3
cos 150 = cos (180−30) = − cos 30 = −
	2

	−√3+1
2cos2 75 =
	2

podziel przez 2 i pierwiastek...bierzesz tylko dodatni bo cos 75 jest dodatni

Jack: aczkolwiek chyba duzo latwiej bedzie sin 45−30 bo nwm czy czegos w tym drugim nie skopalem...latwiej sie tam pomylic

Jack: ano jak mowilem, tam w liczniku powinno byc + 2a nie +1...dlatego polecam pierwsz sposob : D

5-latek: Albo wzor polowkowy

	1		1−cosα
sin		α= √
	2		2

Jack: Małolatku a jakies wyprowadzenie ? : D Byloby mile widziane, bo tak po prostu jest se wzor i o, to wolalbym wiedziec skad jest

5-latek: Pozniej to zrobie Teraz musze zagladnac do zony i wyjść z psem . Zapisze sobie na kartce gigant i wyprowadzenie wzoru .

Jack: dobra juz czaje, nie bylo pytania...to jest po prostu cos 2alfa zamienione Dbaj o nia , dbaj poki mozesz

GIGANT: Ehh no tak. Jak nie twierdzenie cosinusów, to może twierdzenie sinusów. Wystarczyło troche pokombinować. Dzięki wielkie Najgorzej jest załapać o co chodzi, później to już z górki Jeszcze raz dzięki Jack i 5−latek.

Jack: jak cos to tam obliczysz "krotszy bok" i wtedy twierdzenie cosinusow na ten najdluzszy... ewentualnie odrazu nadluzszy z twierdzenia sinusow tylko wtedy masz kąt 105 stopni chyba...ale tak samo sie da ; )

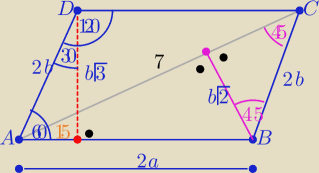
Eta: Na poziomie gimnazjum ( bez trygonometrii i bez wzoru sinusów) b>0 , a>0

	1
P(ABCD)= 2*		*b√2*7= 7b√2 i P(ABCD)= b√3*2a
	2

	7√6
to: 2ab√3= 7b√2 /: b ⇒ 2a√3=7√2 /*√3 ⇒ 2a*3=7√6 ⇒ 2a=
	3

	7√6
Odp : |AB|=2a=
	3