Ekstrema stódętpolskiego: Witam, Mam problem z wyznaczeniem monotoniczności i ekstremów jednej funkcji, tj. f(x) = ln(1−x²). Czy mógłby ktoś to rozwiązać?

Jerzy: zacznij od dziedziny , a potem pochodna

stódętpolskiego: Wiem o tym. Dziedzina to przedział: (−1;1), zaś pochodna to (−2x)/(1−x²)

Jerzy: teraz szukamy miejsc zerowych pochodnej

stódętpolskiego: zgadza się − czyli 0.

Jerzy: teraz zastanów się, czy pochodna w punkcie:x = 0 zmienia znak ( warunek istnienia ekstremum)

stódętpolskiego: W sumie od −1 do 0 jest rosnąca − tak mi się wydaje − także zmienia znak. Czyli w 0 funkcja osiąga swoje maximum − tak?

Jerzy: dokładnie tak

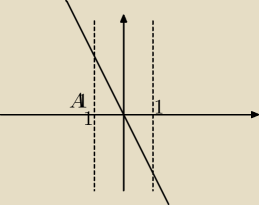
stódętpolskiego: ale mam problem o odczytaniem tego z wykresu. mógłbyś mi pomóc?

Jerzy: rozpatrujemy funkcę: f(x) = −2x ( funkcja liniowa) w przedziale: (−1,0) funkcja: f(x) = −2x jest dodatnia ( pochodna dodatnia,funkcja rośnie) w przedziale: (0,1) funkcja: f(x) = −2x jest ujemna( pochodna ujemna,funkcja maleje)

stódętpolskiego: Dzięki wielkie, rozjaśniło mi to jeszcze bardziej obraz tego wszystkiego. Pozdrawiam i dziękuje jeszcze raz.