analityczna
xxxy: Okrąg o środku S(3,2) leży wewnątrz okręgu o równaniu
(x−6)2+(y−8)2=100
i jest do niego styczny. Wyznacz równanie prostej stycznej do obu okręgów.
Obliczyłam to zadanie, wszyszło mi
b=11−5√5 i b=11+5√5
Chciałabym tylko aby ktoś mi wytłumaczył dlaczego odrzucamy odpowiedź z b=11+5√5 >
14 sty 20:46
5-latek:
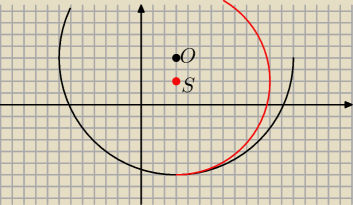
A co to jest b?
czyli te okręgi będą styczne wewnętrznie
ja tego nie liczyłem ale według rysunku prosta ta będzie miała równanie y=−6 9wedlug mnie
14 sty 22:34
xxxy: b to jest współczynnik b w stycznej , odpowiedz to
y=−1/2 x +11 −5√5
14 sty 23:08
5-latek:
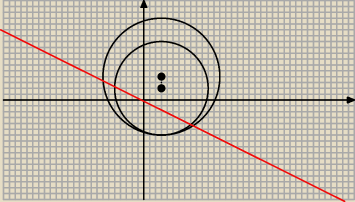
Z rysunku widać ze ta prosta nie jest styczna do obu okregow
Może nie ta odpowiedz
14 sty 23:16
5-latek: No ale skoro taka jest odpowiedz .
Jeżeli b= 11+5√5 to wykres idzie jeszcze do góry
14 sty 23:23
Qulka:
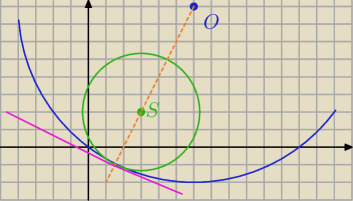
15 sty 03:12
Qulka: odrzucamy, bo wówczas okręgi byłyby styczne na górze i wtedy nie mieściłby się cały w tym
większym
15 sty 03:13
5-latek: dzień dobry
Aniu 
Pozdrawiam
Ale okrag o równaniu
(x−6)
2+(y−8)
2=100 ma srodek O=(3,4) a nie O=(6,8)
15 sty 10:36
Jerzy:
a dlaczego w punkcie: O(3,4) ?
15 sty 10:38
===:
a nasz
małolat jeszcze pod gazem

15 sty 10:38
5-latek: WItam Panow

No tak nie mysle

Przepraszam przecież to już jest postac kanoniczna
15 sty 10:43
 A co to jest b?
czyli te okręgi będą styczne wewnętrznie
ja tego nie liczyłem ale według rysunku prosta ta będzie miała równanie y=−6 9wedlug mnie
A co to jest b?
czyli te okręgi będą styczne wewnętrznie
ja tego nie liczyłem ale według rysunku prosta ta będzie miała równanie y=−6 9wedlug mnie
 Z rysunku widać ze ta prosta nie jest styczna do obu okregow
Może nie ta odpowiedz
Z rysunku widać ze ta prosta nie jest styczna do obu okregow
Może nie ta odpowiedz

 Pozdrawiam
Ale okrag o równaniu
(x−6)2+(y−8)2=100 ma srodek O=(3,4) a nie O=(6,8)
Pozdrawiam
Ale okrag o równaniu
(x−6)2+(y−8)2=100 ma srodek O=(3,4) a nie O=(6,8)

 No tak nie mysle
No tak nie mysle  Przepraszam przecież to już jest postac kanoniczna
Przepraszam przecież to już jest postac kanoniczna