Geometria Krzysiek: Na przyprostokątnych BC i CA trójkąta prostokątnego ABC zbudowano, po zewnętrznej stronie, kwadraty BEFC oraz CGHA. Odcinek CD jest wysokością trójkąta ABC. Wykaż, że proste AE, BH oraz CD przecinają się w jednym punkcie.

Eta: Kto "łapie" to zadanie? ( bo nie chcę na darmo się opisać i rysować

Mila: Pisz.

Eta: Hej Mila Pisz....... bo przyszła do mnie sąsiadka ... (na pogaduchy

Krzysiek: Mila

Krzysiek: Eta ?

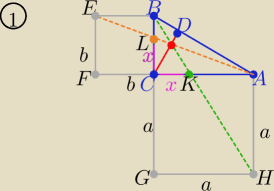
Eta: 1/ wykazujemy,że |CL|=|CK| z podobieństwa trójkątów EFA i LCA z cechy (kkk)

	b		b+a		ab
		=		⇒ x=
	x		a		a+b

analogicznie z podobieństwa trójkątów HGB i KCB z cechy (kkk)

	a		a+b		ab
		=		⇒ x=
	x		b		a+b

zatem : |CL|=|CK|=x

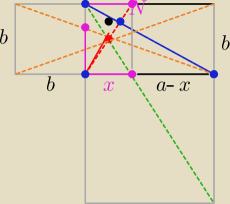
Eta: 2/ Ciężko jest mi tu o dokładny rysunek (oznacz punkty jak na poprzednim i dodaj komentarz: 1/ odkładamy odcinek x otrzymując prostokąt ( ten mały po środku jego przekątne w tym BK ( zawarta w HB i wysokość AD zawarta w przekątnej CN przecinają się w punkcie M 2/ dorysowujemy odcinek długości a−x otrzymując prostokąt o bokach a+b jego przekątne w tym AE przecinają się w punkcie M wniosek ... kończy dowód Może Mila poda inny sposób

Mila: Skorzystać z tw. odwrotnego do tw. Cewy. Wykorzystać to co napisała Eta 02:11 Napisać? czy wystarczy Ci dowód Ety?

Mila: Cevy.