ekstrema Theosh: ekstrema

	x−2
Witam mam obliczyć ekstrema i przedziały monotoniczności funkcji
	x2

	x2−4x+4
Pochodna to :		x0 = 2
	x4

No i wychodzi mi że jest stale rosnąca i znak pochodnej się nie zmienia, to znaczy że nie ma ekstremum?

Jack:

	x2 − 2x(x−2)		x2 − 2x2 + 4x		−x2+4x
f ' (x) =		=		=
	x4		x4		x4

mi taka pochodna wyszla

Theosh: źle policzyłem pochodną. zaraz poprawiam.

Theosh: wiecie jak wygląda ekstremum rej funkcji? Wyznaczyłem już przedziały w których pochodna jest większa i mniejsza od 0

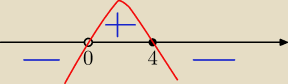
Jack: kontynuujac pochodna mozna skrocic, w sensie jeden iks...

	4−x
czyli mamy		teraz przyrownujemy do zera
	x3

x³ (4−x) = 0 x ≠ 0 4 −x = 0 x = 4 ekstremum lokalne w 4 − maximum

	1
f(4) =
	8

Monotonicznosc : 1) x∊ ( − ∞ ;0) f ' (x) < 0 , funkcja maleje 2) x∊(0;4> f ' (x) > 0, funkcja rosnie 3) x∊ (4;∞) f ' (x) <0 funkcja maleje

Theosh: no i tak zrobiłem dzięki Mogę dać jeszcze jeden przykład?

Jack: tak, ale szybciutko : D

Theosh: (1−2x)e^x D=R pochodna: e^x(3−2x) e^x jest zawsze dodatnie dlatego znak zależy od 3−2x I dalej licze, ale nie wiem czy mam pochodną dobrze.

Jack: ; o ło panie, ja w liceum jestem, nie wiem co to jest "e" lepiej zaloz nowy post to ktos Ci podpowie : D

Theosh: już ogarniam źle policzyłem pochodną znowu(lol)

Jack: aczkolwiek pochodna z (1−2x)*e^x to bedzie −e^x(2x+1)

	1		2
ekstremum powinno wyjsc dla x= −		i wynosi
	2		√e

Theosh: tak mi wszystko wyszło dzięki jack

Jack: