geometria majeczka: Ostrosłup ABCS o podstawie ABC będącej trójkątem równobocznym i wysokości SD gdzie D jest środkiem odcinka AB, przecięto płaszczyzną równoległą do płaszczyzny podstawy. Punkty E, F, G są punktami wspólnymi płaszczyzny przekroju i krawędzi bocznych ostrosłupa. Punkty E', F', G' leżą na podstawie ABC i odcinki EE', FF', GG' są do niej prostopadłe. Wiedząc, że AB=12 i SD=16 oblicz w jakiej odległości od płaszczyzny podstawy należy poprowadzić przekrój ostrosłupa aby graniastosłup E'F'G'EFG miał największą objętość. zadanie, które treścią przeraża. ktos ma pomysł?

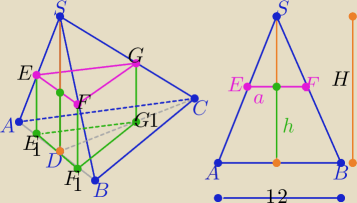Eta: h −−− dł. wysokości graniastosłupa |EF|=a−−− dł. boku podstawy graniastosłupa ( trójkąta równobocznego) Z podobieństwa trójkątów ABS i EFS z cechy (kkk)

	12		16		3
		=		⇒ a= 12−		h , h∊(0,16)
	a		16−h		4

	a2√3
V(graniastosłupa) =		*h
	4

	√3
V( h)=		(12−0,75h)2*h
	4

V^'(h)= ....................... V^'(h)=0 ⇔ ....................... h_max=............. .............................. dokończ już samodzielnie