pochodna joozek: Udowodnij, że wielomian nie mia pierwiastków rzeczywistych: f(x)=3x¹0−5x⁶+3 czyli f(x)>0 I chcę to zrobić z pochodnych f'(x)= 30x⁹−30x⁵ f'(x)=0 30x⁹−30x⁵=0 30x⁹=30x⁵ nie jest prawdziwe, więc nie ma pierwiastków rzeczywistych f'(x)= 30x⁹−30x⁵ f'(x)>0 30x⁹−30x⁵>0 30x⁹>30x⁵ jest prawdziwe, więc nie ma pierwiastków rzeczywistych Czy któreś rozumowanie jest poprawne? a jeśli nie to jak to zrobić?

Kacper: Żadne z powyższych nie jest poprawne.

jola: czyli jak to zrobić? mółbyś pomóc?

Jack: 30x⁹ = 30x⁵ co tu jest nie prawdziwe... jak Ty wgl to cos rozwiazujesz ; o ... Poprawnie : 30x⁹ −30x⁵ = 0 30x⁵ (x⁴ − 1) = 0 x = 0 lub x⁴ − 1 = 0 (x²−1)(x²+1) = 0 x= −1 lub x = 1 zaznaczasz te 3 miejsca zerowe i ekstrema minima ...

ax: 30x⁹−30x⁵=0 30x⁵(x⁴−1)=0 x₁=0 x₂=−1 x₃=+1

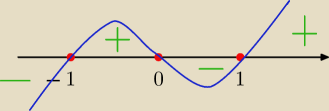
Jack: jak widac minimum jest w −1 i w 1 f(−1) = f(1) = 1