Trygonometria Kolega: √2 cos ^x₂ = 1 Rozpisałem to tak, że podzieliłem przez √2 i wyszło mi cos ^x₂ = ^√2₂ i co z tym teraz?

Jack: cosinus jest √2{2} dla 45 stopni oraz dla (360−45) = 315 stopni czyli

x		π		x		π
	=		+ 2k π lub		= π −		+2 k π , gdzie k ∊ C
2		4		2		4

oblicz iksa

Jack: w drugim przypadku "wkradl sie chochlik" tam powinno byc

x		π
	= 2π −		+ 2k π
2		4

Kolega: dzieki wielkie właśnie nie widziałem co z tym ^x₂ bo mi ta 2 "przeszkadzała"

Jack: nie, czekaj, cos jest nie tak, sie nie zgadza

Kolega: pierwsze sie zgadza w drugim powinno byc x= − ten pierwszy wynik ale spokojnie ja wszystko wiem nie wiedizałem jak rozpisać ^x₂

Jack: tak, cos z tym drugim skopalem...

Kolega: Jack mam jeszcze jedno pytanie jak mam sin(2x− ^π₃ )= −1 to jak rozpisać to w środku?

Jack: tak samo...

	π
sin(2x −		) = −1
	3

kiedy sin x = −1

	3
dla x =		π o ile dobrze pamietam
	2

więc

	π		3
2x −		=		π + 2k π, gdzie k ∊C
	3		2

Kolega: Teraz rozumiem, dzieki wielkie

Jack: apropo, tamto dobrze mialem : D w sensie post 19:33

x		π
	= 2π −		+ 2 kπ
2		4

	π
x = 4π−		+ 4kπ
	2

	7
x =		π + 4kπ
	2

teraz jak bym podstawil k = −1

	π
x = −		+ 4kπ
	2

Kolega: x= ³₂π to wziałęś z wykresu czy jak? Jak inaczej tez mozna obliczyć, że bedzie akurat te ³₂π

Kolega: już wiem skad to jest, ale zaćmienie...

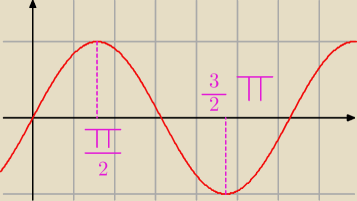
Jack: z wykresu...

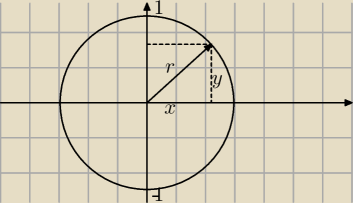
5-latek: Albo z kola trygonometrycznego o promieniu R=1 i z określenia

	y
sinx=
	r