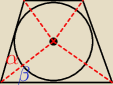
Trapez opisany na okręgu matematyk97: Jeżeli trapez jest opisany na okręgu to odcinki poprowadzone do wierzchołków podzielą kąt na połowę(α=β)? Ehh, ta dzisiejsza matura

Metis: Środek okręgu wpisanego leży na przecięciu dwusiecznych. Zatem kąty α i β są...

matematyk97: Dzięki, tak tylko chciałem się upewnić

Metis: Trudna była?

matematyk97: Mnie przerosła Do tego głupie błędy. Jednokładność nie wiem gdzie powaliłem, bo wyszło mi k=−1 I najśmieszniejsze... W tym dowodzie za 3 pkt, z trójkątem prostokątnym rozpisałem sin3x nie z tego wzoru (nie wiem jakim cudem) i nie chciało wyjść.

Metis: Ja nie pisałem U mnie szkoła coś w tym roku zawaliła próbne . Pisałem tylko z Operonu, której poziom nie był taki jakiego się spodziewałem.

matematyk97: Nowa Era się postarała 18 zadanek w 180 minut Ehh Nie ma co, tylko trzeba zacząć bardziej ostro się przygotowywać

Jack: ja na rozszerzeniu mialem 19 zadanek...

matematyk97: Może mi się coś pomyliło, ale jakoś dużo było, i jak Ci poszło?

Jack: nie nie, ja mialem z oke...ty miales pewno nowa ere...

matematyk97: No tak, kiedy tą OKE pisałeś? Dzisiaj?

Jack: yesterday

Jack: na szescie zadanka z trygonometrii sa zawsze latwe : D

matematyk97: Już próbnych żadnych raczej nie będzie?

Jack: a za malo Ci ? : D

matematyk97: No jak my jeszcze jednego działu nie zaczęliśmy CKE mogłoby wydać jakiś realny arkusz

Jack: ja 3 nie mam ; )

Jack: miales jakies trudne zadanko ?

matematyk97: Hmm, trudne może nie za bardzo, ale się zastanawiałem czy da radę to pogrupować: Udowodnić, że wielomian nie mia pierwiastków rzeczywistych: f(x)=3x¹⁰−5x⁶+3 Więc jednak zrobiłem to z pochodnych.

Jack: skoro udowodnic ze nie ma rzeczywistych to jak chcesz pogrupowac ; D tylko chyba z pochodnej...

matematyk97: No powinno się dać

Qulka: (x²−1)²(3x⁶+6x⁴+4x²+2)+1 kwadrat •same plusy i parzyste wykładniki +1 zdecydowanie większe od 0