oblicz wartości pozostałych funkcji trygonometrycznych kąta x Ajis: oblicz wartości pozostałych funkcji trygonometrycznych kąta x ctgx=⁵₁₂ i x ∊ (0; ^π₂) ctgx= ^−√5₂ i x ∊ (^π₂;π)

Janek191:

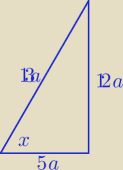
	5		π
ctg x =		i x ∊ ( 0;		)
	12		2

	5 a		5
cos x =		=
	13 a		13

	12 a		12
sin x =		=
	13 a		13

	12
tg x =
	5

Ajis: Tutaj trzeba użyć takiego wzrou 1+ctg²x= ¹_sin²x

5-latek:

	1
no to sin2x=		wylicz z tego sinx i x∊(0,π)
	1+ctg2x

5-latek:

	1
I sprawdz sobie czy to jest prawda 1+ctg2x=
	sin2x

	1
a także 1+tg2x=
	cos2x

Julka: sinx=2/3 gdzie x∊π/2,π

6latek:

	π
x∊(		π)
	2

sinus + cosinus (−) tg (−) ctg (−)

	√5
cosx= √1−sin2x= −
	3

	sinx
tgx=		podstaw i policz
	cosx

	1
ctg x =		to samo
	tgx