Geometria qqaazzxx: Na trójkącie ABC, o bokach długości 6,8,12 opisano okrąg. Na okręgu obrano jeszcze 3 punkty A1,B1 i C1 tak, że powstał sześciokąt wypukły, jakie maxymalne pole może mieć ten sześciokąt? Wyliczym tylko, że pole trójkąta ABC jest równe √455 i R=144/√455 i tak się zastanawiam czy ten pieciokąt A1B1C1AB to fragment sześciokąta foremnego i nie mam pomysłu na to zadanie

Janek191: Sześciokąt foremny powinien mieć największe pole.

qqaazzxx: No tak ale to nie będzie konkretnie sześciokąt foremny, bo ten trojkat ABC nie jest równoramienny

Janek191: Ale tutaj nie da się tak dobrać punktów A₁,B₁, C₁

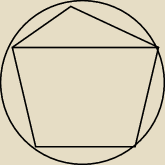
qqaazzxx: Ale pieciokąt A1B1C1AB może być fragmentem sześciokąta foremnego

qqaazzxx: Oj nie taki rysunek