geometria
KASIA: W trójkącie równoramiennym kąt przy wierzchołku ma miarę 120 stopni. Wyznacz stosunek długości
promienia okręgu opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten
trójkąt.
16 gru 19:45
KASIA: ?
16 gru 20:01
onaa:
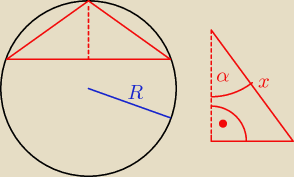
| x | |
| =2R ( to jest zależność z twierdzenia sinusów) |
| sin90 | |
więc stosunek 1:2
16 gru 20:28
onaa:

| x | |
| =2R ( to jest zależność z twierdzenia sinusów) |
| sin90 | |
więc stosunek 1:2
16 gru 20:29
KASIA: ale to ma być stosunek promienia okręgu opisanego do promienia okręgu wpisanego.
16 gru 20:42
KASIA: ale to ma być stosunek promienia okręgu opisanego do promienia okręgu wpisanego.
16 gru 20:43
KASIA: i to koniec? a skąd wiem jaki jest promień okręgu wpisanego

16 gru 20:44
KASIA: i to koniec? a skąd wiem jaki jest promień okręgu wpisanego

16 gru 20:44
KASIA: i to koniec? a skąd wiem jaki jest promień okręgu wpisanego

16 gru 20:46
%2525253Cb%2525253EKASIA%2525253A%2525253C%2525252Fb%2525253E%25252520i%25252520to%25252520koniec%2525253F%25252520a%25252520sk%252525C4%25252585d%25252520wiem%25252520jaki%25252520jest%25252520promie%252525C5%25252584%25252520okr%252525C4%25252599gu%25252520wpisanego%25252520%2525253Cimg%25252520style%2525253D%25252522margin-bottom%2525253A-3px%25252522%25252520src%2525253D%25252522emots%2525252F2%2525252Fpytajnik.gif%25252522%2525253E%2525250A%2525250A
16 gru 20:48
onaa: wiesz w ogóle na jakiej zasadzie obliczyłam R

korzystam z zależności trójkąta
16 gru 20:55
onaa:
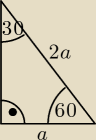
ier
16 gru 20:57
onaa: ten ostatni bok ma dłgość a√3
16 gru 20:57
onaa: wzór na pole trójkąta z którego można obliczyć mały promień P=p*r
p−połowa obwodu trójkąta
wzór na pole trójkąt z którego mozemy teraz skorzystać P=a*b*sinα czyli
16 gru 21:00
onaa: | | 1 | | 2x+x√3 | |
teraz licze połowę obwodu: p= |
| (x+x+x√3)= |
| |
| | 2 | | 2 | |
podtaw teraz to wszystko do pierwszego wzoru na pole trojkata
16 gru 21:03
onaa: r=2x
√3−3x
| | | | R | |
więc stosunek promieni jest równy |
| = |
| |
| | 2x√3−3x | | r | |
16 gru 21:07





 korzystam z zależności trójkąta
korzystam z zależności trójkąta
 ier
ier