wykresy funkcji Leszek: Witajcie, potrzebuję narysować komputerowo wykresy tych funkcji, ale... żaden program nie uwzględnia dziedziny. Jakaś rada?

	x5 − 1
a) f(x) =
	x4 − x2 − 4

	ln(1 + ex2+1)
b) f(x) =
	x

https://matematykaszkolna.pl/forum/rysunek118479.png Co prawda Mila pomogła mi (raz jeszcze dziękuję) z innym przykładem, acz muszę to zrobić komputerowo. Niestety zbytniego rozeznania w forumowym "rysowniku" nie posiadam, więc czy mógłbym prosić o narysowanie tychże funkcji? Pozdrawiam serdecznie

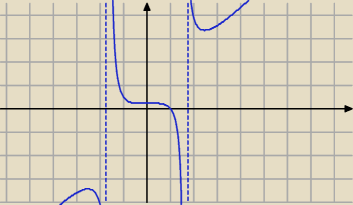utem: x⁴−x²−4=0

	√1+√17		√1+√17
x1=		≈1,6 lub x2=−		≈−1,6
	√2		√2

lim _x→x1−f(x)=−∞ lim _x→x1+f(x)=∞

	−1		1
f(0)=		=
	−4		4

x=1 miejsce zerowe Asymptoty pionowe:

	√1+√17
x=
	√2

	√1+√17
x=−
	√2

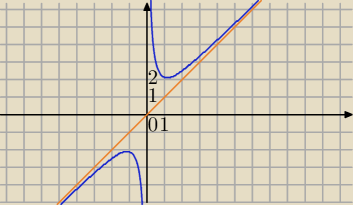utem: Jest tam asymptota ukośna w (a), ale musisz obliczyć granice y=x b) x≠0 x=0 asymptota pionowa Asyptoty ukośne :

	ln(1+ex2+1
limx→∞		=1 ( H)
	x2

y=x+b

	ln(1+ex2+1
b=lim{x→∞}[x−		]=0
	x

y=x http://calcoolator.pl/rysowanie_wykresow_funkcji.html