Geometria analityczna Nick: 2. Dana jest prosta k: y = –x + 6, która przecina oś OY w punkcie A. Przez punkt P(4, 2) poprowadzono prostą l, która przecięła oś OY powyżej punktu (0, 2) i poniżej punktu A. Suma pól dwóch trójkątów powstałych między prostymi k, l oraz osiami układu współrzędnych jest równa 6. Napisz równanie prostej l.

Nick: Up

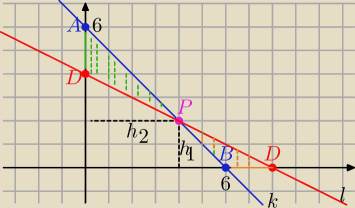
Eta: k: y= −x+6 B, A∊k to A(0,6) i B( 6,0) P∊l to: l : y= a(x−4)+2 ⇒ l: y=ax−4a+2 , b= −4a+2 z treści zadania b>2 i b<6 ⇒ −4a+2>2 i −4a+2<6 ⇒ a∊(−1,0) h₂=4 i h₁=2

	1		1
P(ADP)=		*4*|AD| , P(DBP)=		*2*|BD|
	2		2

z treści zadania : (**) 2|AD|+|BD|= 6 |AD|= |6−(−4a+2)|= 4|a+1|

	4a−2		2		2
ax−4a+2=0 ⇒ x=		= 4−		, D(4−		, 0)
	a		a		a

	2		a+1
|BD|= |4−		−6| = 2|		|
	a		a

	a+1
to z (**) 8|a+1|+2|		|=6 /:2
	a

	a+1
i dla a∊(−1,0) 4(a+1) −		=3 /*a ⇒ 4a2+4a−a−1=3a ⇒ 4a2−1=0
	a

	1		1		1
(a−		)(a+		)=0 i a∊(−1,0) to a= −
	2		2		2

	1
zatem prosta L ma równanie: y= −		(x−4)+2
	2

	1
l: y=−		x+4
	2