Obliczanie działań sinusów tena: 3*sin ^pi₅ + 4*sin ^2pi₅ + 5*sin ^3pi₅ + 6*sin ^4pi₅ = Wynik to 13.8496. Czy dałoby radę te działanie jakoś skrócić?

tena: Nie widać tego mianownika w ułamkach. Wszystkie to 5.

5-latek:

	π
sin		= sin36o= ...zobacz w tablicach
	5

	2π
sin		= sin72o = znasz sin36 podwojony sin36
	5

	3π
sin		= sin108 o (tutaj wzory redukcyjne
	5

	4π
sin		= sin144o
	5

Qulka: oj 5−latku sin72 ≠ 2 sin36 tylko 2sin36cos36

Qulka: a jeśli pierwszy z tablic to spokojnie pozostałe również bo nie ma sensu robić jedno w przybliżeniu a pozostałe dokładnie

tena: Które jest w przybliżeniu?

Qulka: to odczytane z tablic

tena: Aaaa już rozumiem. To pierwszy sposób, a jest jakiś drugi?

Bogdan: Jest inny sposób, w którym nie odczytuje się wartości z tablic. Początek

	3π		2π		4π		π
Stosujemy toższmości: sin		= sin		, sin		= sin
	5		5		5		5

Otrzymujemy:

π

2π

2π

π

π

2π

3sin

+ 4sin

+ 5sin

+ 6*sin

= 9sin

+ 9sin

= ...

5

5

5

5

5

5

5-latek: Dzien dobry Qulka Pozdrawiam O tym myslalem ale napisałem tak jak napisałem

tena: Bogdan Dzięki. Potem jak dalej to rozpisać?

5-latek:

	3π		2π
No to napisz dlaczego sin		= sin		?
	5		5

5-latek: Witaj Bogdan Mnie się tez to przydalo co napisales bo teraz wlasnie w międzyczasie powtarzam trygonometrie

tena: Podejrzewam, że na podstawie jakiegoś wzoru. Dla mnie tak to wygląda:

	3π		π		2π
sin		− sin		= sin
	5		5		5

5-latek: Otoz Ogolnie to wynika z rozwiązanie podstawowego równania sinx=a

tena: Muszę się nauczyć takie działania rozwiązać. Proszę mi uwierzyć, zależy mi na zrozumieniu Czyli to było podstawienie?

tena: Jak było to podstawienie, to potem trzeba do tego wrócić? Nie wiem, co to jest a Dla mnie to wygląda jak podstawienie

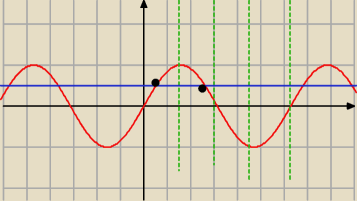
5-latek: Nie nie podstawienie Narysuj sobie wykres y=sinx i zauważ ze w ramach jednego okresu i w przedziale −1<a<1 każdej wartości a odpowiadają dwa kąty masz narysowany wykres y=sin(x) i prosta y=0,5 Teraz widać ze w okresie 2π sa dwa rozwiązania

5-latek: Może niezbyt zrozumiale dlaCiebie to napisałem Ale pewnie już rozwiazylawes równania trygonometryczne i np. takie rownie

	1		1
sinx=		i to		= a
	2		2

Bogdan: Podaję przydatne wartości:

	π		2π		√5 − 1
sin18o = sin		= cos72o = cos		=
	10		5		4

	π		3π		√5 + 1
cos36o = cos		= sin54o = sin		=
	5		10		4

	π		2π		√ 10 + 2√5
cos18o = cos		= sin72o = sin		=
	10		5		4

	π		3π		√ 10 − 2√5
sin36o = sin		= cos54o = cos		=
	5		10		4

A może ktoś spróbuje wyznaczyć te wartości (takie zadanie mogłoby się pojawić w arkuszu maturalnym na poziomie rozszerzonym). W podanym tu zadaniu mamy wynik

	π		2π		√ 10 − 2√5		√ 10 + 2√5
9(sin		+ sin		) = 9(		+		) = 13,84957592...
	5		5		4		4

tena: Dziękuję. Takie gotowe wzory można znaleźć w necie albo wyczytać z tabelki. Chciałbym wiedzieć, jak to się wyznacza.

Bogdan: Zaproponowałem wyliczenie tych wartości, może tegoroczni maturzyści spróbują?

tena: Może ja spróbuję. Poproszę o wskazówkę.

	2π
Obliczymy sin
	5

Jakiś wzór do tego? sin²x?

Bogdan: Podczas matury nikt wskazówek nie będzie udzielał

tena: Jestem po maturze

Eta: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=2018

Bogdan:

Eta:

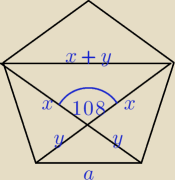
Bogdan: Pięciokąt foremny.

	x		x + y
Korzystamy z własności tej figury:		= φ, (a także		= φ),
	y		a

	√5 + 1		y		√5 + 1
φ − złota liczba, φ =		,		=
	2		x		2

cos108^o = −cos72^o Na podstawie tw. cosinusów: (x + y)² = 2x² + 2x²cos72^o

	y		y
x2 + 2xy + y2 = 2x2(1 + cos72o) /:x2 ⇒ 1 + 2*		+ (		)2 = 2(1 + cos72o)
	x		x

	1 + 2φ + φ2		(1 + φ)2
cos72o =		− 1 ⇒ cos72o =		− 1
	2		2

	√5 + 1		√5 − 1
Po zastosowaniu φ =		otrzymamy cos72o =
	2		4

sin72^o obliczymy korzystając z jedynki trygonometrycznej.

tena: Mam pytanie, czy te wartości można policzyć korzystając z pięciokąta, ponieważ w mianowniku jest 5?

Bogdan: Sprecyzuj pytanie. O mianownik którego ułamka Ci chodzi?

tena: Tego działania w pierwszym poście. Wszystkich ułamków.

Bogdan:

	π		2π
36o =		, 72o =
	5		5

	π		2π
O 13:13 podałem wynik Twojego działania: 9sin		+ 9sin
	5		5

	π		2π
Kontynuując to działanie otrzymujemy: 9(sin		+ sin		) = ...
	5		5

Mając obliczoną wartość cos72^o obliczymy sin72^o z jedynki trgonometrycznej. Ponadto korzystając z zależności: cos2α = 1 − sin²α obliczymy sin36^o: cos72^o = cos(2*36^o) = 1 − sin²18^o. Tyle w tej sprawie z mojej strony. Dobranoc