pochodna z pochodnej ola: Mam zadanie z przebiegu zmiennosci funkcji, do 1 pochodnej wydaje mi sie ze mam dobrze. potem licze pochodna z pochodnej i wydaje mi sie ze zle mi wychodzi F(x)=¹_1+x² F`(x)=^−2x_(x²+1)² F``(x)=<sup>6x4+4x2−2</sup><sub>(x<sup>2</sup>+1)<sup>4</sup></sub> przyrównuje F``(x)=0. przujmuje parametr t=x² i t>0 t=1/3 czyli a w zadaniu powinno mi wyjsc t=3

Qulka: jakbyś używała dużego U do ułamków byłoby coś widać

ola: juz poprawiam

	1
f(x)=
	x2+1

	−2x
f`(x)=
	(x2+1)2

	6x4+4x2−2
f``(x)=
	(x2+1)4

olekturbo: −2(x²+1)²−2(x²+1)*2x*(−2x) to licznik f''(x)

Qulka: wszystko ok

ola: i teraz gdy przyrównuje licznik f``(x)=0 6x⁴+4x²−2=0 x²=t , t>0 6t²+4t−2=0 delta=64

	−4+8		1
t=		=
	12		3

	1
x2=
	3

i tak mi wychodzi...

Qulka: mi też

ola: a w zadniu powinno wyjsc x²=3 z tego x=√3 lub x=−√3

	1		1
stad f(√3)=		lub f(−√3)=−
	4		4

ola:

	1
blad, dla f(−√3)=
	4

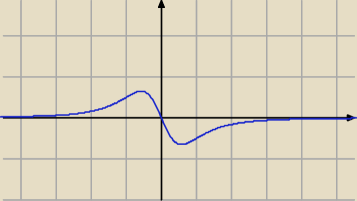
Qulka: jak widać ekstrema pochodnej, czyli miejsca zerowe drugiej pochodnej są poniżej 1 więc na pewno nie √3

ola: czyli dobre jest moje liczenie? bo robie to juz ktorys raz i jakies glupoty mi wychodzą... Mogłby ktoś dokończyc to zadanie od tej drugiej pochodnej? akurat ten przyklad bede miec prawdopodobnie na kolokwium i cos robie chyba zle...

Qulka: no masz dobrze x=+− √3/3

ola:

	√3
i teraz rysuje wykres f``, wypukłości, wklęsłości, punkty przegięcia dla x=+−
	3

	3
wychodzi dla obu x=
	4

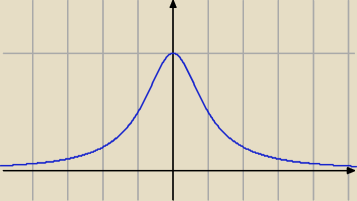
Qulka: tak wygląda

ola: to jest wykres drugiej pochodnej czy juz koncowy?

Qulka: wykres funkcji

ola: wykre funkcji ma tak wygladac, y(max)=1 (z wczesniejszych obliczen) ma rosnac od nieskonczonosci do zera− malec od zera do nieskonconosci ale nigdy nie przetnie osi OX ale na

	1		1
wykresie w odpowiedzi mam zaznaczone pp dla x=√3 y=		i dla x=−√3=		a nam pp
	4		4

wyszly inne...

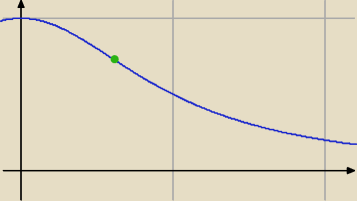
Qulka: jak widać z krzywej pp jest w zielonym