planimetria Mat: Wykaż, że jeśli stosunek promienia okręgu wpisanego w trójkąt prostokątny do promienia okręgu opisanego na tym trójkącie jest równy √2 − 1, to trojkąt ten jest równoramienny. Próbowałem r/R=[1/2(a+b+c)] /(1/2c); ostatecznie otrzymałem ze r/R=(a+b−c)/c.... i co dalej, ktoś coś?

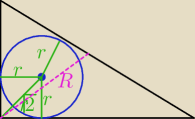
Qulka: wtedy R=(√2+1)r zatem środkowa jest wysokością czyli jest równoramienny

Mat: Wybacz, ale troche za szybko dla mnie, dalej nie rozumiem jak mam połączyć to co napisałem z Twoim R. Możesz troszeczkę dokładniej rozpisać?

Mat: Nie rozumiem tego "zatem środkowa jest wysokością" . Ja próbowałem porównać (a+b−c)/c do √2 − 1, i otrzymałem, że 2R=c... ale chyba nic z tego nie wynika

Qulka: jak widać na obrazku jak R = √2r +r to wtedy ta różowa się pokrywa z zieloną więc środkowa =R (różowa) jest równa wysokości (bo r jest prostopadłe)