analityczna Qulka: Czy tylko mi się wydaje że to zadanie jest praktycznie nierozwiązywalne http://www.zadania.info/d549/7857580 Wyznacz wartość parametru m, dla której pole koła stycznego do boków AB i CD równoległoboku ABCD o wierzchołkach A = (5,− 4) , B = (2 ,− 8 ) , C = (m³ + 15m ,m⁴ + 10m²) jest najmniejsze możliwe. Oblicz to pole.

misiak: dlaczego? okrąg ma być styczny tylko do jednej pary boków równoległoboku

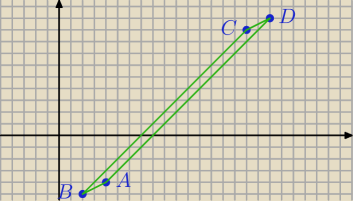
Qulka: ale tu konkretnie do AB i CD i wprawdzie nie bardzo mi się zmieściło ale nawet w takiej skróconej wersji sobie tego nie umiem wyobrazić

PW: A dla m < 0?

Qulka: ale jak znaleźć to najmniejsze? bo jak wzięłam prostopadłą to wredne wyniki wyszły

Kacper: Tam masz rozwiązanie

Qulka: a czy narysowałeś sobie to rozwiązanie to powiedz mi gdzie jest to kółeczko, bo mi wyobraźni brakuje

Qulka: i nie ma odważnych żeby się zmierzyć z 4 potęgą

Qulka: a oni to kwalifikują jako maturalne .. a nasi maturzyści omijają szerokim łukiem

Ajtek: A jak to narysować Ten okrąg Qulka, ten rysunek to chyba do bani jest.

wmboczek: No przecież to łatwe minimalna odległość C od prostej AB wynosi 2r tylko min okazuje się max przy || czy jakoś tak

Qulka: wmboczek to to oblicz mi proszę i narysuj wynik

Qulka: Ajtek ten obrazek to mniej więcej ich wynik obliczony na zasadzie minimalnej odległości C do prostej AB tzn. jak podstawię obliczone m=1

Ajtek: Aha, to mniej więcej mnie zmyliło.

Qulka: nie dało się zmieścić ale sens oddałam że wynik bez sensu i powtarzać maturzystom że analityczną się zaczyna od rysunku

Ajtek: Bo się zaczyna, tylko z punktem C są problemy, D to przesunięcie o wektor.

Metis: To jest kwestia sporna Jeśli rozwiązuje coś analitycznie to staram się pod żadnym pozorem nie robić rysunku, w końcu to przewaga analitycznej nad geometrią na płaszczyźnie. Ale okazuje się, że czasami, a nawet często rozwiązanie zadania z analitycznej bez rysunku pomocniczego, a nawet realnego, oddającego dane przedstawione w zadaniu jest niemożliwe i wtedy się denerwuję, że nie jestem taki dobry, by zauważyć tego bez rysunku

Mila: Nie patrzę na takie koszmarki, gdy nie muszę. Pamiętasz Ajtek, tę bryłówkę z kulą styczną do krawędzi sześcianu bodajże?

Mila: Metis , rysunek w geometrii to podstawa i wszystko widzisz.

Metis: Tak, Milu. Ale profesor zwraca uwagę na to, że w geometrii na płaszczyźnie zadanie rozwiązujemy na podstawie rysunku. Na początku go rysując. A w geometrii analitycznej rysunek jest ważny, bo przedstawia nasz tok myślenia− oznaczenia itp. ale jest "ukoronowaniem" zadania. Najpierw liczymy, a na końcu robimy piękny rysunek oddający sens i właściwość naszych obliczeń.

Ajtek: Hej Mila, szczerze mówiąc to nie pamiętam. Mój pomysł na to zadanie, nie rozwiązywałem tego, to zlokalizować prostą CD. Mamy punkt C, D zaś to przesunięcie o wektor zgodny z [BA]→. Takie luźnie rozmyślania wieczorne.

Ajtek: Słuchajcie, ja uciekam spać, jak nic nie zrobicie, to pomyślę nad tym jutro. Spokojnej Wszystkim!

Qulka: mi wyszły baaardzo brzydkie pierwiastki

Metis: Qulka, a o którym zadaniu w ogóle mowa? Pogubiłem się. Przecież to zadanie jest rozwiązane na zadania.info

Qulka: ale to rozwiązanie tam jest rozwiązaniem bez sensu co widać na poglądowym rysunku powyżej .. i jestem ciekawa czy się da poprawnie je rozwiązać

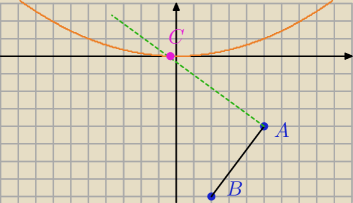
wmboczek: no ja rozwiązałem i byłem zadowolony że poprawnie a tu guzik żeby nie powiedzieć Qulka rozwiązanie widzę tak: krzywa parametryczna na punkt C ma normalną, której a=−3/4 liczymy dla jakiego m wybieramy to m, dla którego −13/2<b<−1/4 (a czy jest takie i co jak nie ma?) fajne zadanie ale raczej na jakiś konkurs dla studentów

Qulka: ja próbowałam że C może być na prostej prostopadłej do AB przechodzącej przez A ..ale próba rozwiązania tego to masakra http://www.wolframalpha.com/input/?i=-3%28m%5E3+%2B+15m%29-1%3D4%28m%5E4+%2B+10m%5E2%29

Qulka:

wmboczek: graficznie z wykorzystaniem Geogebry P≈1,69π Nad A punkt D, punkt C o wektor w prawo od D

wmboczek: http://zapodaj.net/41a2f6460f25e.png.html

piotr1973: http://www.wolframalpha.com/input/?i=distance+between+point+%5Bm%5E3%2B15%2Cm%5E4%2B10m%5E2%5D+and+line++y%3D-32%2F3%2B%284+x%29%2F3

wmboczek: @piotr1973 − czytałeś w czym problem? TAK zrobiła większość ale jest to niemożliwe geometrycznie czyżby jakiś bug w Wolframie? połączył 60m−32 w 28?

PW: Komuś się po...myliło, jeżeli takie zadanie uznał za maturalne. Rozumiem tok rozumowania w zadania.info (pierwszy post Qulki), ale jest to rozumowanie życzeniowe − autor rozwiązania zakłada (nigdzie tego nie sprawdzając ani nie pisząc tego wprost), że taki okrąg istnieje− chyba tylko dlatego, że pytają o to. Nie trzeba dużej wyobraźni, żeby narysować równoległobok, dla którego nie istnieje opisany w zadaniu okrąg styczny, i nie ma to nic wspólnego z odległością wierzchołka od przeciwległego boku.

Qulka: wmboczek to graficznie jest pewnie tak samo przybliżone jak moje ale dodatkowo Twój równoległobok nazywa się ABDC

wmboczek: oczywiście dokładnie się nie da Swoją drogą ABCD to chyba opis dowolnego czworokąta bez precyzowania boków? Zwyczajowo punkty nazywamy kolejno Ciekawe jak by było z ocenianiem zadania: "Dane są punkty A=(1,−2), B=(3,0), C=(4,5). Wyznacz punkt wiedząc, że ABCD jest równoległobokiem"

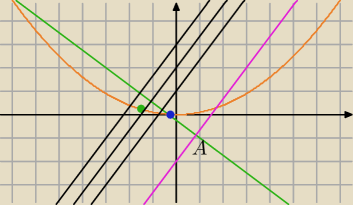
henrys: hmmm PW, wydaje mi się, że taki okrąg nie istniałby wtedy i tylko wtedy gdyby krzywa, do której należy punkt C znajdowała się powyżej prostej prostopadłej do AB. Z warunków zadania, jest tak jak napisała Qulka, żeby jego odległość od AB była najmniejsza musi należeć do prostej prostopadłej do AB. Im mniejsza pierwsza współrzędna punktu C, tym druga współrzędna jest coraz większa, zatem i odległość od AB jest coraz większa, więc C musi być punktem przecięcia prostej prostopadłej do AB i podanej krzywej. Równanie będzie miało rozwiązanie, więc okrąg istnieje. Problem tylko ze znalezieniem tego rozwiązania.

Qulka: po kliknięciu w wolframie na dokładną postać ... ułamek ma 4 liniki http://www.wolframalpha.com/input/?i=-3%28m%5E3+%2B+15m%29-1%3D4%28m%5E4+%2B+10m%5E2%29

PW: Nie wiem, henrys, nie zastanawiałem się nad tym, jak poprawnie rozwiązać zadanie. Zwracałem tylko uwagę, że autor rozwiązania w zadania.info przyjął jako oczywiste, że skoro pytają, to taki okrąg istnieje. Ani nie napisał kiedy istnieje, ani nie sprawdził, czy okrąg o wyliczonym przez niego promieniu rzeczywiście jest styczny do obu boków. Rozważania typu (cytuję) "Im mniejsza pierwsza współrzędna punktu C, tym druga współrzędna jest coraz większa", zupełnie mnie nie przekonują. Maturzysta na pewno nie spojrzy na współrzędne punktu C w ten sposób, że C należy do pewnej krzywej. Nie uczy się w szkole o takich krzywych. Ci którzy podają jakieś ilustracje, korzystają z programów komputerowych, a przecież nie na tym polega rozwiązywanie zadania maturalnego. Zadanie jest na tyle trudne, że − jak widać − nawet jasne określenie warunków rozwiązywalności sprawia kłopoty.

Qulka: po zgłoszeniu uwag poprawili treść zadania więc jakby ktoś kiedyś wykopał ten post to już nieaktualny

PW: I to jest Twój sukces Nieraz narzekacie, że "czepiam się" sformułowań w treściach zadań albo w rozwiązaniach. Okazuje się jednak, że stare marudy czasem marudzą nie bez przyczyny

kyrtap:

Qulka: a dziękuję wprawdzie myślałam, że może zmienią równanie na C żeby dało się po prostu znaleźć pierwiastki, ale skoro jest w dziele ekstremum to zrobili z niego takie typowe zadanie na ekstremum

jakubs:

ngl: Pomożecie udowodnić to równanie?

	a2+b2		a+b
√		≥
	2		2

zef:

	a2+b2
2√		≥a+b //2
	2

2a²+2b²≥a²+2ab+b² 2a²+2b²−a²−b²−2ab≥0 (√2a+√2b)²+2ab−a²−b²≥0 (√2a+√2b)²−(a−b)²≥0

Jack: To jeat nierownosc miedzy srednimi... Ps. Zaloz wlansy post...

Jack: Zef...jak masz postac 2a² + 2b² − a² − b² −2ab ≥0 To przeciez to jest a² + b² − 2ab≥0 (a−b)²≥0

ngl: Dziękuję bardzo i przepraszam, że pod postem na inny temat.. każdy miał kiedyś swój pierwszy raz na forum