Odległość punktu od prostej. big ben: Wyznacz równanie prostej, do której należy punkt P(1, −1) i takiej,, że odległość punktu Q(8, −2) od tej prostej wynosi 5.

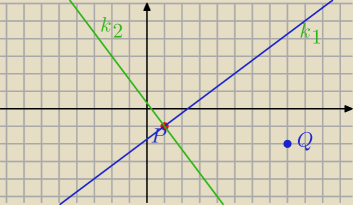
utem: P=(1,−1)∊k k: y=ax+b −1=a+b, b=−1−a k: y=ax−a−1⇔ax−y−a−1=0 d(Q,k)=5 5=U{|a*8−1*(−2)−a−1|}{√a²+1⇔ |8a+2−a−1|=5*√a²+1 |7a+1|=5*√a²+1 /² 49a²+14a+1=25a²+25 24a²+14a−24=0 licz dalej sam

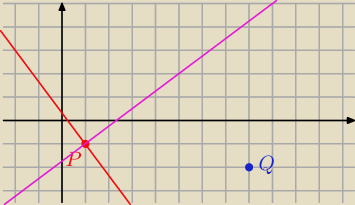Janek191: y = a x + b − 1 = a + b ⇒ b = − 1 − a czyli y = a x − 1 − a a x − y − 1 − a = 0 ============ d = 5 i Q = ( 8 ; − 2) więc

	I 8 a + 2 − 1 − a I
		= 5
	√ a2 + 1

I 7 a + 1 I = 5 √a² + 1 zatem 7 a + 1 = 5 √a² + 1 lub 7 a + 1 = − 5 √a² + 1 49 a² + 14 a + 1 = 25 a² + 25 24 a² + 14 a − 24 = 0 / : 2 12 a² + 7 a − 12 = 0 Δ = 49 − 4*12*(−12) = 49 + 576 = 625 √Δ = 25

	− 7 − 25		4
a =		= −		lub a = U{3}[4}
	24		3

więc

	4		1		3		7
b = − 1 +		=		lub b = − 1 −		= −
	3		3		4		4

	4		1		3		7
y = −		x +		lub y =		x −
	3		3		4		4

============================

Janek191: Niepotrzebnie się opisałem

utem: Szkoda, że nie ma okienka, w którym byłoby widać, że ktoś już rozwiązuje.

big ben: dzięki