1)Dwa wierzchołki prostokąta leżą na osi OX, a dwa pozostałe - nad osią OX i nal Gienek: 1)Dwa wierzchołki prostokąta leżą na osi OX, a dwa pozostałe − nad osią OX i należą do paraboli y=6−x². Na rysunku widać, że A(−t,0), B(t,0) a)Podaj wzór wielomianu opisującego pole tego prostokąta w zależności od t, Jaka jest dziedzina tej funkcji? Wzor obliczylem P=−2t³+12t a jak dziedzine funkcji ustalic?

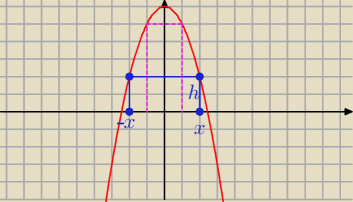
Janek191: A = ( − x; 0) B = ( x; 0) C = ( x; 6 − x² ) P = I A B I *h = 2x*(6 − x²) = 12 x − 2 x³ P(x) = −2 x³ + 12 x ============== y = 6 − x² = 0 ⇔ x² = 6 ⇔ x = − √6 lub x = √6 Dziedzina funkcji P(x): ( 0 ; √6 )