Oblicz pole zacieniowanego obszaru.Koło,geometria analityczna.
Adam :
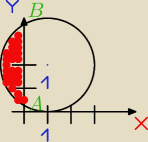
Oblicz pole zacieniowanego obszaru.
Z wcześniejszych zadań mam równanie okręgu: (x−1)
2 + (y−2)
2 = 4
oraz punkty przecięcia z osią OY A(0, 2 −
√5 ) B(0, 2 +
√5 )
Jest już na forum rozwiązane to zadanie,ale sposób jakim jest rozwiązane jest za ciężki.Da się
to zrobić prościej?Geometria analityczna część 1 ksiązki(liceum 1 kl./technikum 1 i 2 kl.)
10 sty 20:03
Janek191:
Od pola wycinka koła odejmujemy pole trójkąta.
10 sty 20:08
Adam : Jakie pole trójkąta,jaki wycinek.Nie mam kąta żeby zrobić wycinek a i tak wycinki,których
uczono mnie w szkole zaczynały się od środka okręgu i rozchodziły się na dwa punkty na okręgu.
10 sty 20:10
Janek191:
Połącz środek koła z punktami A i B.
10 sty 20:11
Adam : A skąd mam znać kąt żeby wyliczyć wycinek?
10 sty 20:26
utem:
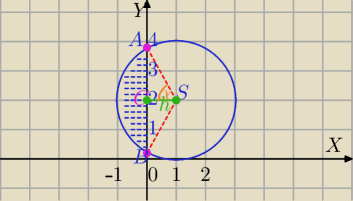
S=(1,2)
(x−1)
2 + (y−2)
2 = 4
Punkty przecięcia z OY:
x=0
(0−1)
2+(y−2)
2=4
(y−2)
2=3
y−2=
√3 lub y−2=−
√3
y=2+
√3 lub y=2−
√3
A=(0,2+
√3)
B=(0,2−
√3)
|AB|=|2+
√3−(2−
√3)|=2
√3
W ΔCSA:
α=60
o
Kąt środkowy ASB ma miarę 120
o.
10 sty 20:30
Janek191:

10 sty 20:35
Adam : |AB|=|2+√3−(2−√3)|=2√3
Dlaczego moduł?
Nie powinno być:
lABl = √(0−0)2 + (2+√3 − (2−√3)2 ?
10 sty 21:31
utem:
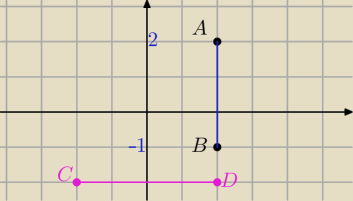
To przecież to samo wyjdzie . Moduł bo długość odcinka jest dodatnia..
W pionie i poziomie możesz liczyć odejmując współrzędne.
|AB|=|2−(−1)|=3
albo
|AB|=|−1−2|=3
|CD|=|−2−2|=4 albo |CD|=|2−(−2)|=4
10 sty 21:49
Adam : Ostatnie pytanie:
Jak obliczyłeś,że α=60o ?
10 sty 22:07
utem:
Masz tam napisane, liczę cosinus kąta w ΔCSA.
( to jest zresztą trójkąt, gdzie przyprostokątna jest 2 razy mniejsza od
przeciwprostokątnej, było w gimnazjum)
10 sty 22:30
misiak:
nie trzeba wyznaczać współrzędnych punktów A i B.
Wystarczy obliczyć długość cięciwy z tw. Pitagorasa
(0,5d)2+12=22
(0,5d)2=3
0,5d=√3
d=2√3
10 sty 22:42
utem:
Można i tak, akurat wyznaczenie wsp.A i B jest proste.
10 sty 22:50
Adam : Wszystko zrozumiałe, dzięki Panowie.Zapomniałem o tych własnościach sinusów itp.
10 sty 22:53
utem:
10 sty 22:54
 Oblicz pole zacieniowanego obszaru.
Z wcześniejszych zadań mam równanie okręgu: (x−1)2 + (y−2)2 = 4
oraz punkty przecięcia z osią OY A(0, 2 − √5 ) B(0, 2 + √5 )
Jest już na forum rozwiązane to zadanie,ale sposób jakim jest rozwiązane jest za ciężki.Da się
to zrobić prościej?Geometria analityczna część 1 ksiązki(liceum 1 kl./technikum 1 i 2 kl.)
Oblicz pole zacieniowanego obszaru.
Z wcześniejszych zadań mam równanie okręgu: (x−1)2 + (y−2)2 = 4
oraz punkty przecięcia z osią OY A(0, 2 − √5 ) B(0, 2 + √5 )
Jest już na forum rozwiązane to zadanie,ale sposób jakim jest rozwiązane jest za ciężki.Da się
to zrobić prościej?Geometria analityczna część 1 ksiązki(liceum 1 kl./technikum 1 i 2 kl.)
 S=(1,2)
(x−1)2 + (y−2)2 = 4
Punkty przecięcia z OY:
x=0
(0−1)2+(y−2)2=4
(y−2)2=3
y−2=√3 lub y−2=−√3
y=2+√3 lub y=2−√3
A=(0,2+√3)
B=(0,2−√3)
|AB|=|2+√3−(2−√3)|=2√3
S=(1,2)
(x−1)2 + (y−2)2 = 4
Punkty przecięcia z OY:
x=0
(0−1)2+(y−2)2=4
(y−2)2=3
y−2=√3 lub y−2=−√3
y=2+√3 lub y=2−√3
A=(0,2+√3)
B=(0,2−√3)
|AB|=|2+√3−(2−√3)|=2√3

 To przecież to samo wyjdzie . Moduł bo długość odcinka jest dodatnia..
W pionie i poziomie możesz liczyć odejmując współrzędne.
|AB|=|2−(−1)|=3
albo
|AB|=|−1−2|=3
|CD|=|−2−2|=4 albo |CD|=|2−(−2)|=4
To przecież to samo wyjdzie . Moduł bo długość odcinka jest dodatnia..
W pionie i poziomie możesz liczyć odejmując współrzędne.
|AB|=|2−(−1)|=3
albo
|AB|=|−1−2|=3
|CD|=|−2−2|=4 albo |CD|=|2−(−2)|=4