Równania i nierówności [F[Miśka]]: Witam, mam dwa zadania i chciałabym by ktoś sprawdził czy są one poprawnie zrobione 1)Dla jakich wartości parametru m równanie − x²+3x+|x−4|=m ma tylko jedno rozwiązanie. Moje rozwiązanie:

	⎧	x−4,x≥4
|x−4|=	⎩	−x+4, x<4

x≥4 x<4 −x²+3x+x−4=m lub −x²+3x−x+4=m −x²+3x+x−4−m=0 −x²+2x+4−m=0 Δ=16−4(4+m)=16−16−4m=0 x2−2x−4+m=0 4m=0 m=0 Δ=4+4(4−m)=4+16−4m=20−4m=0 4m=20 m=5 dla x≥4 m=0 dla x<4 m=5 2) Rozwiąż nierówność

	x2
|		| < 1
	x2−4

Moje rozwiązanie: x²−4≠0 (x−2)(x+2)≠0 D=R/{−2,2}

	x2		−x2
1o		−1<0 2o		−1<0
	x2−4		x2−4

	4
		<0 U{−2x2+4)(x2−4}
	x2−4

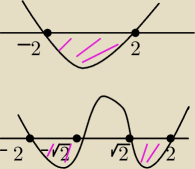
(x−2)(x+2)<0 −2(x²−2)(x−2)(x+2)<0 x∊(−2,2) x∊(−2,−√2)(√2,2} (Wykresy wyżej) Czyli x∊(−2,−√2)(√2,2)

Kacper: Strasznie dużo przepisywania masz gadu?

[F[Miśka]]: 6110782

[F[Miśka]]: Halo halo, sprawdzi ktoś?

[F[Miśka]]: To drugie już wiem że mam źle, i fajnie by było jakby ktoś mi poradził jak je zrobić

Jack: Pierwszy wyglada na ok

Jack: aczkolwiek daj mi chwile, bo cos chyba nie tak ; D

5-latek: Wlasnosc wartości bezwzględnej |x|<a ⇔gdzy x<a I x>−a Już widzisz co masz zle ? To jedno Poza tym

P(x)
	< > ≤≥0 to P(x)*W(x)<>≤≥0
W(x)

Jack: ok, pierwsze bedzie ok, drugie

	x2
|		| <1
	x2−4

1) 2)

x2		x2
	< 1 /\		> − 1
x2−4		x2−4

Czyli sie zgadza z twoim, tylko na koniec bierzesz /\ czyli część wspólną obu

Marcin: W pierwszym zadaniu narysuj wykres funkcji i z niego zobacz rozwiązanie. W drugim zadaniu jak opuszczasz wartość bezwzględną to zmieniasz znak na przeciwny.Lewej strony

	x2		x2
nie zmieniaj. Czyli będzie		<1 i		> −1 Teraz to rozwiązujesz.
	x2−4		x2−4