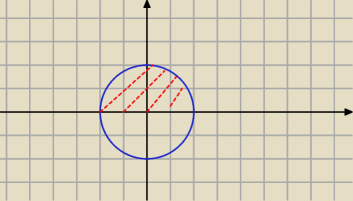
Sprawdzenie RJS: Wyznaczanie promienia całka mam obszar x²+y²≥4 y≥0 0≤r≤2 0≤φ≤π ?

zombi: Chyba x²+y² ≤ 4?

RJS: No faktycznie to będzie ok ?

zombi: Jasne promień 2 i mniejszy, więc się zgadza. Obrót od 0 to 180 stopni pasi.

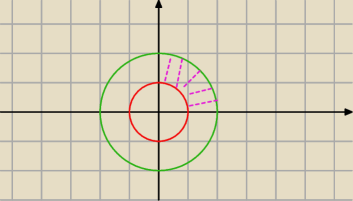
RJS: 1≤x²+y²≤4 x≥0 y≥0 Tutaj nie wiem jak opisać ? 1≤r≤2 ?≤φ≤?

zombi: Robimy cały obrót o 0^o do 360^o, to w jakim zakresie jest fi?

RJS: Ale czemu w całym zakresie ? x≥0 y≥0

Saizou :

	π
Przecież φ zmienia się od 0 do		w zacieniowanym obszarze
	2

RJS: a nie od 0 do π ? Cały czas mam z tym problem

Saizou : nie, przecież jesteśmy tylko w pierwszej ćwiartce, to jak możemy brać φ z zakresu [0;π]

RJS: a np jak by było x²+y²≤9 x≥0 czyli tak samo 0, do π/2 ?

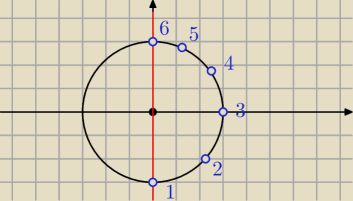
Saizou : no nie, bo tutaj jak mamy ograniczenia obchodzi nas koło o S(0,0), r=3 , ale tylko dla dodatnich x (na prawo od prostej x=0) żeby to opisać musimy zacząć w niebieskiej kropce nr 1 , przejść przez wszystkie kropki i skończyć na 6, wiec jaki to będę kąty ?

RJS: π/2 do 3π/2 ?

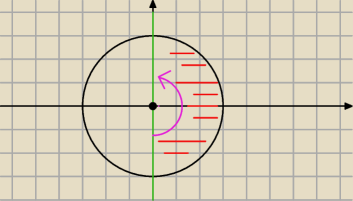
Saizou : to akurat opisuje tą drugą połówkę nas interesuje ten różowy kąt czyli.... PS. Pamiętaj że istnieje coś takiego jak kąty ujemne

RJS: Ehh czyli od 3π/2 do π/2 w tym wypadku jeszcze 5 przykładów

Saizou :

	π		π
jeszcze nie, może powiem jaka jest odp. −		≤φ≤
	2		2

RJS: Jutro wrócę do tego, będzie na forum od rana ?

Saizou : może raczej tak koło 10, 11

RJS: ok, dziękuję za pomoc dziś !