wyznacz wzor f kwadratowej pata: Wyznacz wzor funkcji kwadratowej f w postaci ogolnej, wiedzac ze zbiorem wart. Tej funkcji jest przedxial (−∞;1> a wartosc −5 przyjmuje dla dwoch argumentow 2 i 10.

pata: Wyszlo mi, ze f(x)= −x²−4x−3 Moglby ktos to sprawdzic ?

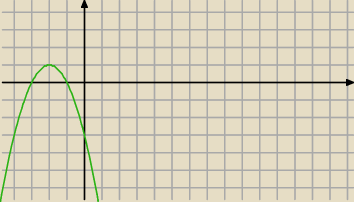
Ajtek: Coś nie tak.

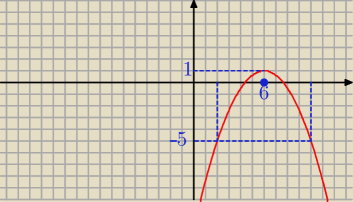
Janek191: q = 1 a < 0 f(2) = f(10) = − 5

	2 + 10
p =		= 6
	2

więc f(x) = a*(x − p)² + q = a*(x − 6)² + 1 a*(2 − 6)² + 1 = − 5 16 a = − 6

	3
a = −
	8

	3
f(x) = −		*(x − 6)2 + 1
	8

Janek191:

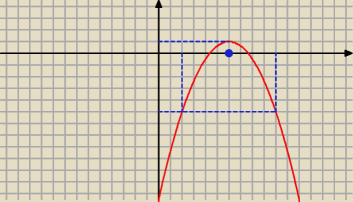
	3		3		9		27		2
f(x) = −		*( x2 − 12 x + 36) + 1 = −		x2 +		x −		+
	8		8		2		2		2

	3		9		25
f(x) = −		x2 +		x −
	8		2		2

============================

pata: Zgubilam minusa tam powinien byc przedzial (−∞,−1>

Ajtek: Nawet gdyby, to nadal Twoje rozwiązanie jest błędne. Na moim rysunku masz przedstawioną funkcję y=−x²−4x−3.

pata: Juz znalazlam blad, dzieki!

Jolanta: y_w=1

	−b
xw=
	2a

	x1+X2		2+10
xw=		=		=6
	2		2

	−b
6=		b=−12a
	2a

−5=a*2²+b*2+c 1=a*6²+b*6+c −5=4a−24a+c 1=36a−72a+c /*(−1) −5=4a−24a+c −1=36a−c −6=16a

	3
a=−
	8

	−29
c=
	2

	9
b=
	2

Jolanta: to dopisz tego minusa i licz