| 2√2 | ||
W trójkącie ostrokątnym dane są: a=2, b=1, sinalpha = | . Oblicz c. | |
| 3 |
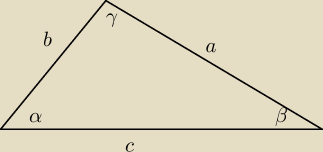a=2
b=1
| 2√2 | ||
sinα= | ||
| 3 |
| a | b | ||
= | |||
| sinα | sinβ |
| b*sinα | 2√2 | √2 | ||||
sinβ= | = | /2= | ||||
| a | 3 | 3 |
| √7 | ||
cosβ=+√1−sin2β=√1−(2/9)= √7/9= | (trójkat ostrokatny | |
| 3 |
| 1 | ||
cosα=+√1−sin2α=√1−(8/9)=√1/9= | ||
| 3 |
| sinα | 2√2 | 1 | 2√2 | |||||
tgα= | = | / | = | *3=2√2 | ||||
| cosα | 3 | 3 | 3 |
| a*sinβ | a*sinγ | |||
tgα= | lub tgα= | |||
| c−a*cosβ | b−a*cosγ |
| a*sinβ | ||
c−a*cosβ= | ||
| tgα |
| √7 | ||
c−2* | =(2*√2/3) /(2√2) | |
| 3 |
| 2√7 | 2√2 | 1 | ||||
c− | = | * | ||||
| 3 | 3 | 2√2 |
| 2√7 | 1 | |||
c− | = | |||
| 3 | 3 |
| 1 | 2√7 | 1+2√7 | ||||
c= | + | = | ||||
| 3 | 3 | 3 |
| 1+2√7 | ||
Odp. Trzeci bok trójkata ma dlugość | [jm] | |
| 3 |
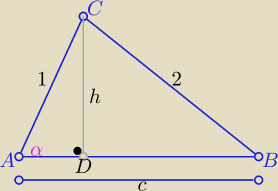
| 2√2 | 2√2 | |||
sinα= | to h= | |||
| 3 | 3 |
| 1 | 2√7 | |||
|AD|= | i | DB|= | |||
| 3 | 3 |
| 1+2√7 | ||
c= | ||
| 3 |
No tak . Prościej i nie ma potrzeby korzystać z tych twierdzeń .
Póżniej jeszcze będe chciał dopytac do tego zadania . Pozdrawiam
| α | β | γ | ||||
sinα+sinβ+sinγ=4cos | *cos | *cos | ||||
| 2 | 2 | 2 |