Monotoniczność i ekstrema funkcji
Nastepny : f(x)=xe1−2x
Wyznaczyć ekstremum funkcji i zbadaj jej monotoniczność.
Proszę krok po kroku, z góry bardzo dziękuje chce to zrozumieć.
8 sty 20:23
Janek191:
D = ℛ
f '(x) = 1*e1 − 2 x + x*( e1 − 2 x) ' = e1 − 2 x + x*e1 − 2x * (−2) =
= e1 − 2x − 2 x*e1 − 2 x = ( 1 − 2 x)*e1 − 2 x
Dla jakiego x jest f ' (x) = 0 ?
8 sty 20:33
Janek191:
[ f(x)*g(x) ] ' = f '(x) * g(x) + f (x) * g '(x) − pochodna iloczynu funkcji
8 sty 20:34
Nastepny : no dla jakiego ?

8 sty 20:35
Janek191:
To ja się pytam

x = ?
8 sty 20:36
Nastepny : x=1/2 ?
8 sty 20:38
Janek191:
Tak

A kiedy f '(x) < 0 ?
8 sty 20:40
Nastepny : no własnie kiedy ?
8 sty 20:41
Janek191:
Nie rób sobie jaj, tylko odpowiadaj

8 sty 20:42
Nastepny : nie mam pojęcia

8 sty 20:43
Janek191:
Kiedy 1 − 2 x < 0 ? ( bo e1 − 2 x > 0 )
8 sty 20:49
Nastepny : aaa to o to chodzi ?

że z tego e musimy wykładnik stwierdzić ?
8 sty 20:50
piotr: 1) dziedzina: x∊R
2) Granice na krańcach dziedziny:
limx−>−∞ xe1−2x = −∞
limx−>+∞ xe1−2x = 0 − asymptota pozioma
miejsce zerowe funkcji w x=0
3)Pochodna:
(xe1−2x)` = (1−2 x)e1−2x
f`(x)>0 dla x<1/2 f(x)↗ rosnąca
f`(x)<0 dla x>1/2 f(x)↘ maleją
miejsce zerowe pochodnej w x=1/2
druga pochodna: 4(x−1)e1−2x dla x=1/2 jest ujemna więc maksimum : f(1/2)=1/2
miejsce zerowe drugiej pochodnej x=1, punkt przegięcia
dla x<1 funkcja f(x) wklęsła, dla x>1 wypukła
8 sty 21:00
Janek191:
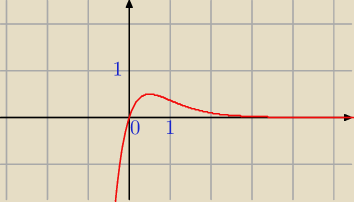
8 sty 21:22
Następny: | | 1 | |
w odpowiedziach jest minimum lokalne właściwe dla x= |
| |
| | 2 | |
8 sty 21:53
Janek191:
Komuś się pomyliło, bo jest odwrotnie − wykres

Co to za zbiór zadań ?
8 sty 22:13

 x = ?
x = ?
 A kiedy f '(x) < 0 ?
A kiedy f '(x) < 0 ?


 że z tego e musimy wykładnik stwierdzić ?
że z tego e musimy wykładnik stwierdzić ?



 Co to za zbiór zadań ?
Co to za zbiór zadań ?