nierówność z wartością bezwzgledną
[Z[Karolcia]]: Rozwiązałam tą nierówność |x−5|−|x−2|≤≤3
rozpisałam trzy przypadki dla x należącego od (−∞,2), drugi <2,5) i trzeci <5,+∞)
w odpowiedziach jest ze x nalezy od (−∞,0> a mi natomiast wyszo ze x należy do R
w swoich obliczeniach nie znalazłam błędu, wiec nie wiem czy zupełnie obrałam złą metode czy
jest błąd w odpowiedziach
8 sty 19:41
Jack: Dobrze mowisz, sa 3 przedzialy
Pokaz obliczenia jakos

8 sty 19:42
[Z[Karolcia]]: I przedział
−x+5+x−2≤3
3≤3 prawidziwe
czyli wszytskie liczby z przedziału I
II przedział
−x+5−x+2≤3
−2x≤−4
x≥2 czyli x nalezy <2,5)
III przedziału
ł x−5−x+2≤3
−3≤3− prawda czyli znów wszytskie liczy z przedziału III
8 sty 19:48
Jack:
1 przedzial tak jak mowisz, wszystkie liczby z pierwszego przedzialu czyli
x ∊ ( − ∞ ; 2)
2 przedzial
x ∊ <2;5)
3)
x ∊ <5;∞)
Wychodzi ze x nalezy do R... prawdopodobnie w odp. jest zle...
8 sty 20:04
Jack: na pewno dobrze przepisane?
8 sty 20:06
Karolcia: tak, wszytsko jest okej wiec to pewnie odpowiedzi są błedne, no nic
dziękuję bardzo za pomoc :3
8 sty 20:12
Jack: jak chcesz miec kolorowy nick to musisz go "zarezerwowac" Klikajac "twój nick" (po lewej, pod
"kliknij po wiecej przykladow" i rezerwacja nicka oraz kolor

8 sty 20:13
Mila:
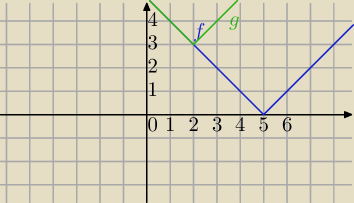
Metoda graficzna.
|x−5|−|x−2|≤3⇔
|x−5|≤|x−2|+3
f(x)=|x−5|
g(x)=|x−2|+3
Wykres f(x) leży poniżej wykresu lub pokrywa się z wykresem funkcji g(x).
x∊R
Metoda algebraiczna :
1)|x−2|=x−2 dla x≥2
2) |x−5|=x−5 dla x≥5
a) x<2 wtedy mamy nierówność:
−x+5−(−x+2)≤3⇔−x+5+x−2≤3⇔3≤3 prawda dla x∊(−
∞,2)
lub
b) x∊<2,5)
−x+5−(x−2)≤3⇔−x+5−x+2≤3⇔−2x≤−4⇔x≥2
Prawda dla x<2,5)
lub
c) x≥5
x−5−x+2≤3⇔−3≤5 prawda dla x∊<5,
∞)
odp.
x∊R
8 sty 20:45
Karolcia: Okej, Jack

Dziękuję

9 sty 10:06
5-latek: A podziekowamia dla Mili ?
9 sty 10:11
Karolcia: wszytskim bardzo dziękuję

9 sty 16:28


 Metoda graficzna.
|x−5|−|x−2|≤3⇔
|x−5|≤|x−2|+3
f(x)=|x−5|
g(x)=|x−2|+3
Wykres f(x) leży poniżej wykresu lub pokrywa się z wykresem funkcji g(x).
x∊R
Metoda algebraiczna :
1)|x−2|=x−2 dla x≥2
2) |x−5|=x−5 dla x≥5
a) x<2 wtedy mamy nierówność:
−x+5−(−x+2)≤3⇔−x+5+x−2≤3⇔3≤3 prawda dla x∊(−∞,2)
lub
b) x∊<2,5)
−x+5−(x−2)≤3⇔−x+5−x+2≤3⇔−2x≤−4⇔x≥2
Prawda dla x<2,5)
lub
c) x≥5
x−5−x+2≤3⇔−3≤5 prawda dla x∊<5,∞)
odp.
x∊R
Metoda graficzna.
|x−5|−|x−2|≤3⇔
|x−5|≤|x−2|+3
f(x)=|x−5|
g(x)=|x−2|+3
Wykres f(x) leży poniżej wykresu lub pokrywa się z wykresem funkcji g(x).
x∊R
Metoda algebraiczna :
1)|x−2|=x−2 dla x≥2
2) |x−5|=x−5 dla x≥5
a) x<2 wtedy mamy nierówność:
−x+5−(−x+2)≤3⇔−x+5+x−2≤3⇔3≤3 prawda dla x∊(−∞,2)
lub
b) x∊<2,5)
−x+5−(x−2)≤3⇔−x+5−x+2≤3⇔−2x≤−4⇔x≥2
Prawda dla x<2,5)
lub
c) x≥5
x−5−x+2≤3⇔−3≤5 prawda dla x∊<5,∞)
odp.
x∊R
 Dziękuję
Dziękuję 
