Monotoniczność i Ekstrema Następny :

	e2
f(x)=
	1−x

Wyznaczyć ekstremum funkcji i zbadaj jej monotoniczność. Proszę krok po kroku, z góry bardzo dziękuje chce to zrozumieć.

Następny : ?

Dawid: Dziedzina wpierw następnie pochodna funkcji

Następny : krok po kroku proszę takie coś nic mi nie wyjaśnia

Dawid: No dziedzinę i pochodną wyznaczyć umiesz ?

maria : tak a dalej ?

Dawid: przyrównaj pochodną do 0 narysuj wykres przybliżony pierwszej pochodnej i z wykresu możesz odczytać monotoniczność i ekstrema

Nastepny : i tu sie gubiee Jeśli możesz zrób to na kartce i wrzuć foto na jakąś stronę muszę to zobaczyć

Janek191: Czy dobrze przepisana jest funkcja ? Może powinno być

	ex2
f(x) =		?
	1 − x

Nastepny : przepraszam e^x <− to w liczniku

Janek191:

	ex
f(x) =
	1 − x

D = ℛ \ { 1} więc

	ex*(1 − x) − ex*(−1)		ex*( 2 − x)
f '(x) =		=		= 0 ⇔ x =2
	( 1 − x)2		( 1 − x)2

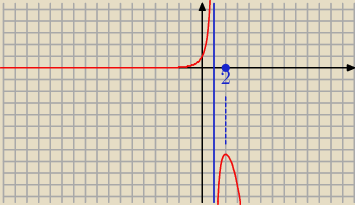
Dla x < 2 jest f '(x) > 0 Dla x > 2 jest f '(x) < 0 więc funkcja f ma maksimum dla x = 2 W ( − ∞ , 1) , w ( 1 , 2) funkcja f rośnie, bo f"(x) > 0 W ( 2 : + ∞ ) funkcja maleje, bo f '(x) < 0 Patrz na wykres

Nastepny : czemu =0 ⇔ x=2 ? i co dzieje się z tym "e²" ?

Janek191: e^x > 0 dla x ∊ℛ ( 1 − x)² > 0 dla x ≠ 1 więc f '(x) = 0 ⇔ 2 − x = 0 ⇔ x = 2

Nastepny : e^x zawsze będzie >0 ? dla X∊R ?

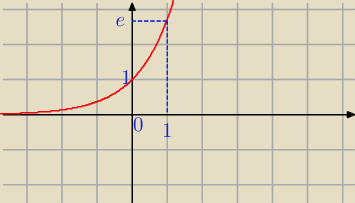
Janek191: f(x) = e^x − funkcja wykładnicza, więc e^x > 0 Patrz na jej wykres.

Nastepny : a jak rysować te wykresy ? Jeśli mozesz wytłumacz

5-latek: Albo na papierze milimetrowym tak jak kiedyś się rysowalo albo teraz w programie rysującym wykresy funkcji