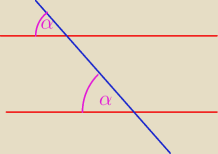
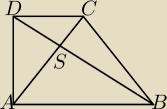
W trapezie prostokątnym ABCD, w którym AB || CD i |AB| = 2|CD|, poprowadzono przekątne AC
i BD, przecinające się w punkcie S. Udowodnij, że odległość punktu S od ramienia AD,
prostopadłego do podstaw, jest trzy razy mniejsza niż długość podstawy AB.
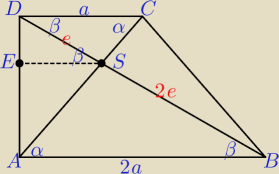
| |AB| | ||
Trójkąty ABS i CDS są podobne w skali k1 = | = 2, stąd |SB| = 2|DS| | |
| |CD| |
| e | 1 | 1 | ||||
Trójkąty ESD i ABD są podobne w skali k2 = | = | ⇒ |ES| = | AB | |||
| 3e | 3 | 3 |
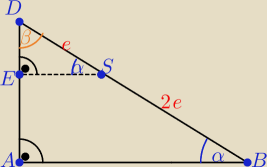ΔABD∼ΔESD z cechy (kkk)
