Środkowa w trójkącie prostokątnym bluffy: W trójkącie prostokątnym ABC punkty A = (−4, 1) i B = (7, −2) są końcami przeciwprostokątnej.

	1		7
Prosta o równaniu y=		x+		zawiera jedną z przyprostokątnych tego trójkąta. Oblicz
	3		3

długość środkowej BS w trójkącie ABC.

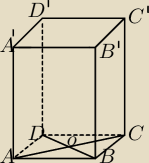
jacks: W graniastosłupie prawidłowym czworokątnym (zobacz rysunek poniżej) punkt O jest punktem przecięcia przekątnych podstawy dolnej, a odcinek OC' jest o 4 dłuższy od przekątnej podstawy. Graniastosłup ten przecięto płaszczyzną przechodzącą przez przekątną BD podstawy dolnej i wierzchołek C' podstawy górnej. Pole figury otrzymanej w wyniku przekroju jest równe 48. Zaznacz tę figurę na rysunku poniżej i oblicz objętość graniastosłupa

wd410: Nie moje zadania, ale może ktoś mógłby coś odpowiedzieć?

wd410:

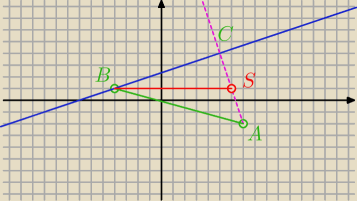
===: banalne ... sam policzy

wd410: A z B chyba zamieniłeś?

wd410:

	1
Niestety nie mam odpowiedzi, ale spróbowałem to zrobić tak: CA to prostopadłe do y=		x +
	3

	7
	3

więc mam: y = −3x + 19 ?

===: y+2=−3(x−7) ⇒ y=−3x+19

===: dalej współrzędne punktu C ... potem środek odcinka CA... a potem już szukane równanie środkowej

wd410: No ok, to teraz mam wszystkie trzy wierzchołki trójkąta. Więc Liczę środek AB i ten obliczam odległość dwóch punktów, S i B, tak?

wd410: C = (³²₅, ⁶⁷₁₅)

===: ... tak .... sądziłem, że pytają o równanie środkowej

===: źle policzone współrzędne punktu C

wd410: 5, 4

wd410:

√250
	?
4

wd410: A to drugie zadanie?

===: ... a mówiłeś, że nie Twoje

===: ... dalej źle liczysz

wd410: nie moje zadanie, szukałem odpowiedzi w google i trafiłem na ten temat bez odpowiedzi.

===: ...skończyłeś to z trójkątem?

wd410: Niestety nie, wziąłem się za następne i te zadania zostawiłem na później. 5 i 4 wyliczyłem, że

	1		5
są to współrzędne punktu C, środek odcinka A i C to (		;		no i podstawiłem do wzoru
	2		2

na odległość dwóch punktów. S i B

===: środek też źle

===: zobacz na rysunku

wd410: No jak? środek odcinka (−4, 1) i (5, 4) ?

===: Ty włącz myślenie Szukasz środka odcinka AC ...

wd410: No ale pisałem ci wczesniej, że A z B zamieniłeś na rysunku.

===: ... przepraszam ... to ja źle oznaczyłem na rysunku

wd410: Ok, niestety nie mam odpowiedzi do tych zadań, więc dlatego tak zawracam głowę Gdybym miał to bym szukał błędu do skutku.