Stereometria
Metis: Stereometria
Cześć

Zaczynam naukę stereometrii. Proszę o
zadanka i małe podpowiedzi do nich.
Od czego zacząć rysunku, co rozpatrywać itp.
Na razie od najprostszych



7 sty 18:51
Mila:
1) W czworościan foremny o krawędzi długości a wpisano kulę.
Obliczyć stosunek objętości tej kuli do objętości czworościanu.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
a) rysunek czworościanu z oznaczeniami.
7 sty 18:57
dero2005:
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są jednakowej długości. Oblicz
miarę kąta α przekątnej ściany bocznej do sąsiedniej ściany bocznej. Oznacz na rysunku kąt α.
7 sty 19:02
dero2005:
W stożek o promieniu podstawy √3 i wysokości 2 wpisano graniastosłup prawidłowy trójkątny w
taki sposób , że dolna podstawa graniastosłupa zawiera się w podstawie stożka , a wierzchołki
górnej podstawy leżą na powierzchni bocznej stożka.Oblicz objętość graniastosłupa wiedząc że
wszystkie jego krawędzie są równej długości. Rys.
7 sty 19:11
Mila:
Dero, ładne zadanka, numeruj, to łatwiej porozumiemy się .
7 sty 19:13
Metis: Dziękuje Wam

Robię po kolei.
7 sty 19:18
Metis: Milu czy na tym rysunku ma znaleźć się ta kula którą wpisujemy?
Jak ją ładnie wykreślic?
7 sty 19:25
7 sty 19:29
dero2005:
3) Podstawą ostrosłupa prostego ABCD jest trójkąt prostokątny ABC, którego przyprostokątne
mają
długość |AB|= 6 cm, |BC| = 8 cm. Wysokość ostrosłupa jest równa 12 cm. Środki krawędzi AB, BC,
CD i AD wyznaczają płaszczyznę przekroju tego ostrosłupa. Oblicz pole przekroju ostrosłupa tą
płaszczyzną.
Odp:6√29
7 sty 19:29
dero2005:
4) Sześcian i ostrosłup prawidłowy czworokątny mają w podstawie kwadrat o boku długości
10. Wiadomo, że objętość ostrosłupa jest równa objętości sześcianu.
a) Wyznacz wysokość ostrosłupa.
b) Oblicz pole powierzchni całkowitej ostrosłupa.
c) Wyznacz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
7 sty 19:32
dero2005:
5) W graniastosłupie prawidłowym czworokątnym przekątna ściany bocznej ma długość 15
cm i tworzy z przekątną graniastosłupa, wychodzącą z tego samego wierzchołka, kąt 30°.
Oblicz objętość graniastosłupa oraz długość jego przekątnej.
7 sty 19:36
wmboczek: @dero2005
w 2) na pewno tyle? w mianowniku 343?
7 sty 19:37
dero2005:
6) Podstawą ostrosłupa jest trójkąt równoboczny o boku długości 3 cm. Spodek wysokości
ostrosłupa jest jednym z wierzchołków podstawy. Ściana boczna, która nie zawiera
wysokości ostrosłupa, jest nachylona do płaszczyzny podstawy pod kątem 45°. Oblicz:
a) wysokość ostrosłupa,
b) objętość ostrosłupa,
c) pole powierzchni całkowitej ostrosłupa,
d) sumę długości wszystkich krawędzi ostrosłupa
7 sty 19:39
dero2005:
7) W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość a. Płaszczyzna przechodząca
przez krawedź podstawy i środek wysokości tego ostrosłupa jest nachylona do płaszczyzny
podstawy pod kątem α. Wyznacz objetość i pole powierzchni bocznej tego ostrosłupa.
7 sty 19:54
5-latek: Metis a dokonczyles tamto zadanie ?
7 sty 19:54
7 sty 19:57
Metis: Jeszcze nie
5−latku 
Muszę złapać podstawy stereometrii bo ostatnio styczność z nią miałem w gimnazjum. Wtedy je
rozwiąże

7 sty 19:57
dero2005:
8) Powierzchnia boczna stożka po rozwinięciu jest półkolem . Kąt rozwarcia tego stożka ma
miarę?
7 sty 19:57
Metis:
Zadanie nr 1 dero2005
α=45o ?
7 sty 19:58
Metis: Obiecuje Ci to
5−latku 
7 sty 19:59
7 sty 20:03
dero2005:
9) Przekątna przekroju osiowego walca jest nachylona do podstawy pod kątem 45 stopni. oblicz
objętość i pole powierzchni całkowitej walca ,jeśli jego przekątna ma długość 18 dm.
7 sty 20:04
dero2005:
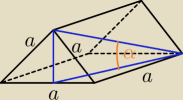
rysunek pomocniczy do zad 1
7 sty 20:11
Metis: dero czytaj posty

7 sty 20:13
dero2005:
Ten rys z 20:03 nie jest do zadania nr 1
7 sty 20:19
Metis: Zadanie 9)
dero
r=45
√2 cm
H=90
√2 cm

7 sty 20:19
Metis: Jest źle?
7 sty 20:21
Mila:
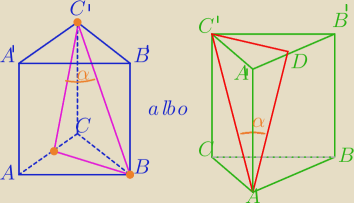
Albo taki rysunek do zadania (1 Dero).
α− kąt między przekątną ściany bocznej BCC'B' a ścianą boczną ACC'A'
∡C'AD− kąt między przekątną ściany bocznej a sąsiednią ścianą boczną.
7 sty 20:23
Metis: A Milu co jest nie tak w moim bo nie widzę błędu.
U mnie ten graniastosłup "lezy" na AA'BB'.
7 sty 20:28
dero2005:
@Metis Do zadania z geometrii czy stereometrii trzeba by zrobić rysunek, zaznaczyć wielkości,
kąty i napisać rozwiązanie a nie podawać fragmentaryczne wyniki

7 sty 20:29
Metis: dero mam wszystko na swoich rysunkach

Potwierdź wynik to wstawię rysunek + obliczenia

7 sty 20:31
dero2005:
Wyniki z 20:19 OK
7 sty 20:38
dero2005:
na rys do zad 1 zaznaczyłeś zły kąt
7 sty 20:41
Mila:
Do rysunku ( zielonego) z 20: 23
|AC'|=a
√2
7 sty 20:41
Mila:
Pisz pełne rozwiązania, to skorygujemy ewentualne błędy.
7 sty 20:42
Mila:
Co z czworościanem z godziny 18:57?
7 sty 20:43
7 sty 20:51
dero2005:
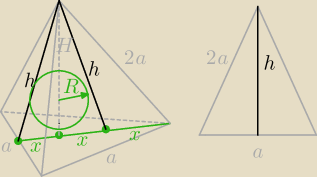
10) Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a,
a krawędź boczna− 2a. Wyznacz promień kuli wpisanej w ten ostrosłup.
rys pomocniczy
7 sty 20:58
Mila: Odp. do zadania 1 z czworościanem.
7 sty 20:58
dero2005:
W zad 9 co innego było do policzenia

7 sty 21:00
Metis: Odpowiedź do zadania 1
dero według zapisu
Mili 20:41
α≈37
o.
Dobrze?

7 sty 21:01
Metis: Wiem
dero ale dalej to już ... "z górki"

7 sty 21:02
Metis: Zadane 1)
Mila
V
k to objętość kuli
V
c objętość czworościanu.
| | a3√2 | |
Vk wyrażamy wzorem: |
| |
| | 12 | |
V
c to szukana objętość kuli.
Z rysunku:
http://i36.tinypic.com/33bd5ck.png
Liczę r.
|OG|=r
Gdzie h to wysokość trójkąta równobocznego o boku a.
I brakuje Nam odcinka OB

7 sty 21:23
Metis: Przepraszam:
Brakuje odcinka |OE|
7 sty 21:24
Metis: |OE| obliczę z podobieństwa trójkątów.
Trójkąt SS'E jest podobny do trójkąta OS'E.
Stąd |S'E|:
| | a√6 | | a√3 | |
( |
| )2+|S'E|2=( |
| )2 |
| | 3 | | 2 | |
7 sty 21:32
7 sty 21:34
Metis: Oczywiscie |S'E| liczę z tw. Pitagorasa a nie podobieństwa.
Z podobieństwa obliczę |OE|
7 sty 21:36
Kacper:

7 sty 22:07
Metis: Co tam
Kacper ?

7 sty 22:11
Kacper:
Zapisuje

7 sty 22:13
Metis: A może rzucisz okiem na moje wywody?

Dobrze liczę r?
7 sty 22:14
Mila:
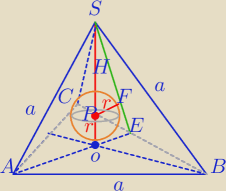
Za bardzo gmatwasz to wszystko. Jak już zrobisz to zadanie, to wypiszę wszystko,
co masz wiedzieć o czworościanie foremnym.
Może narysuję ten rysunek i objaśnię wszystko.
1) podstawa i wszystkie ściany boczne są trójkątami równobocznymi o boku a.
2) Spodek wysokości tego ostrosłupa leży w punkcie przecięcia wysokości Δ
| | a√3 | |
h= |
| długość wysokości podstawy. |
| | 2 | |
H− wysokość ostrosłupa
F, O punkty styczności kuli ze ścianami
| | √8 | | √8 | | a√3 | | a√6 | |
H= |
| h= |
| * |
| = |
| |
| | 3 | | 3 | | 2 | | 3 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
ΔPFS∼SOE
H=4r zapamiętaj tę własność czworościanu foremnego
| | 3 | |
R= |
| H− promień kuli opisanej |
| | 4 | |
==========
dalej to już podstawiasz do wzorów
r
3 licz tak:
| | a√6 | | a√6 | | a√6 | |
r3= |
| * |
| * |
| =? |
| | 12 | | 12 | | 12 | |
Do Jutra. Dobranoc

8 sty 00:24
dero2005:
11) Dany jest ostrosłup prawidłowy trójkątny ABCS, w którym pole przekroju przechodzącego przez
wierzchołek i wysokość podstawy wynosi 12√3. Oblicz pole powierzchni całkowitej i objętość
tego ostrosłupa jeżeli długość krawędzi podstawy wynosi 6 cm.
8 sty 14:32
dero2005:
12) W stożek o wysokości h wpisano walec, którego przekrój osiowy jest kwadratem o boku
długości a, w ten sposób, że oś obrotu stożka pokrywa się z osią obrotu walca. Znajdź objętość
stożka.
8 sty 14:51
dero2005:
13) W graniastosłupie prostym podstawa jest rombem, którego przekątne mają długość 30 i 16 cm.
Dłuższa przekątna graniastoslupa jest nachylona do płaszczyzny podstawy pod kątem 45o. Oblicz
pole powierzchni całkowitej tego graniastosłupa.
8 sty 15:04
Metis: Dziękuje
Milu za analizę

. Dopiero teraz wróciłem do domu − ostatnia próba
poloneza, przenalizuje je i w razie wątpliwości będę pytał

8 sty 18:53
Mila:

8 sty 19:04
Metis: Witaj
Milu widzę że się pojawiłaś, a mam do Ciebie kilka pytanie.
Czy kula która wpisujemy musi mieć punkty styczności wewnątrz ostrosłupa? Z czego to wynika?
Reszta dla mnie zrozumiała, a wyliczenie r i podstawienie do wzorku to tylko obliczenia

9 sty 18:07
5-latek: A jak wpisujesz okrag w trojkat to okrag musi mieć punkty styczności z bokami trojkata ?
9 sty 18:11
Metis: Musi

9 sty 18:13
utem:
Ma mieć punkty styczności z każdą ścianą.
9 sty 19:15
Mila:
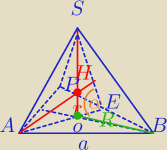
Czworościan foremny o krawędzi a:
| | 1 | |
r= |
| H−promień kuli wpisanej w czworościan foremny. |
| | 4 | |
| | 3 | |
R= |
| H − promień kuli opisanej na czworościanie foremnym |
| | 4 | |
−−−−−−−−−−−−−−−−−r:R=1:3
Wysokości tego ostrosłupa dzielą się w stosunku 1:3. Spróbuj wykazać.
| | a√6 | |
H= |
| , (to wyprowadziłeś) |
| | 3 | |
| | 1 | |
cosα= |
| − cos kąta między ścianami ( wyprowadź ) |
| | 3 | |
11 sty 18:17
Mila:
Zadanie na zastosowanie wiadomości.
Łącząc odpowiednio środki krawędzi czworościanu foremnego otrzymamy ośmiościan foremny.
Krawędź czworościanu ma długość a.
Oblicz objętość ośmiościanu i porównaj ją (ilorazowo) z objętością czworościanu.
11 sty 18:21
Metis: Dziękuje
Milu za pomoc.
Zabieram się do zadań od
dero.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| | 1 | | a2√3 | | a√6 | | a3√2 | |
V= |
| * |
| * |
| = |
| . |
| | 3 | | 4 | | 3 | | 12 | |
11 sty 18:28
Metis:
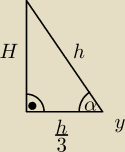
Wyprowadzam cos α:
W naszym trójkącie:
h wysokość trójkąta równobocznego.
11 sty 18:36
Mila:
I po co te rachunki?
Masz zapisane :
| | | | 1 | |
cosα= |
| = |
| i koniec. h nie zmieni się gdy podstawisz , a pomylić się możesz. |
| | h | | 3 | |
Rozwiązuj zadania
Dero.
Jeśli będziesz chciał pomocy, a nie będzie
Dero, to pisz, ale numeruj zadania,
aby nie było nieporozumień.
11 sty 18:55
Mila:
Z ośmiościanem jutro. Narysuj duży ładny rysunek na kartce.
11 sty 18:57
Metis: 
Mam nadzieję, że w II etapie nie pojawi sie zadanie ze stereometrii/prawdopodobienstwa ,
podobnie jak w tamtym roku, ale coś czarno to widzę

11 sty 18:58
Mila:
Kiedy masz II etap?
11 sty 19:15
Metis: 31 styczeń
Gdzie od piątku rozpoczynam ferie.
11 sty 19:16
 Zaczynam naukę stereometrii. Proszę o zadanka i małe podpowiedzi do nich.
Od czego zacząć rysunku, co rozpatrywać itp.
Na razie od najprostszych
Zaczynam naukę stereometrii. Proszę o zadanka i małe podpowiedzi do nich.
Od czego zacząć rysunku, co rozpatrywać itp.
Na razie od najprostszych 


 Robię po kolei.
Robię po kolei.
 Muszę złapać podstawy stereometrii bo ostatnio styczność z nią miałem w gimnazjum. Wtedy je
rozwiąże
Muszę złapać podstawy stereometrii bo ostatnio styczność z nią miałem w gimnazjum. Wtedy je
rozwiąże 

 rysunek pomocniczy do zad 1
rysunek pomocniczy do zad 1


 Albo taki rysunek do zadania (1 Dero).
α− kąt między przekątną ściany bocznej BCC'B' a ścianą boczną ACC'A'
∡C'AD− kąt między przekątną ściany bocznej a sąsiednią ścianą boczną.
Albo taki rysunek do zadania (1 Dero).
α− kąt między przekątną ściany bocznej BCC'B' a ścianą boczną ACC'A'
∡C'AD− kąt między przekątną ściany bocznej a sąsiednią ścianą boczną.

 Potwierdź wynik to wstawię rysunek + obliczenia
Potwierdź wynik to wstawię rysunek + obliczenia 
 Zad 9)
http://i.imgur.com/1PxIfW1.png
Zad 1) dero
Juz poprawiam
Zad 9)
http://i.imgur.com/1PxIfW1.png
Zad 1) dero
Juz poprawiam 
 10) Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a,
a krawędź boczna− 2a. Wyznacz promień kuli wpisanej w ten ostrosłup.
rys pomocniczy
10) Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a,
a krawędź boczna− 2a. Wyznacz promień kuli wpisanej w ten ostrosłup.
rys pomocniczy




 korzystam z rysunku :
http://i36.tinypic.com/33bd5ck.png
korzystam z rysunku :
http://i36.tinypic.com/33bd5ck.png



 Dobrze liczę r?
Dobrze liczę r?
 Za bardzo gmatwasz to wszystko. Jak już zrobisz to zadanie, to wypiszę wszystko,
co masz wiedzieć o czworościanie foremnym.
Może narysuję ten rysunek i objaśnię wszystko.
1) podstawa i wszystkie ściany boczne są trójkątami równobocznymi o boku a.
2) Spodek wysokości tego ostrosłupa leży w punkcie przecięcia wysokości Δ
Za bardzo gmatwasz to wszystko. Jak już zrobisz to zadanie, to wypiszę wszystko,
co masz wiedzieć o czworościanie foremnym.
Może narysuję ten rysunek i objaśnię wszystko.
1) podstawa i wszystkie ściany boczne są trójkątami równobocznymi o boku a.
2) Spodek wysokości tego ostrosłupa leży w punkcie przecięcia wysokości Δ

 . Dopiero teraz wróciłem do domu − ostatnia próba
poloneza, przenalizuje je i w razie wątpliwości będę pytał
. Dopiero teraz wróciłem do domu − ostatnia próba
poloneza, przenalizuje je i w razie wątpliwości będę pytał 



 Czworościan foremny o krawędzi a:
Czworościan foremny o krawędzi a:
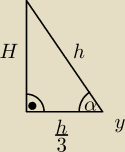 Wyprowadzam cos α:
W naszym trójkącie:
Wyprowadzam cos α:
W naszym trójkącie:
 Mam nadzieję, że w II etapie nie pojawi sie zadanie ze stereometrii/prawdopodobienstwa ,
podobnie jak w tamtym roku, ale coś czarno to widzę
Mam nadzieję, że w II etapie nie pojawi sie zadanie ze stereometrii/prawdopodobienstwa ,
podobnie jak w tamtym roku, ale coś czarno to widzę