Bok kwadratu ABCD ma długość 6 annnnnn: Bok kwadratu ABCD ma długość 6. Na bokch BC i CD wybrano odpowiednio punkty E i F umieszczone tak, że |CE|=2|DF| . Oblicz wartość |DF| dla której pole powierzchni trójkąta AEF jest najmniejsze

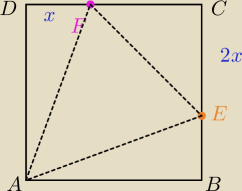
kochanus_niepospolitus: W zadaniu nie jest jednoznacznie określone położenie punktów F i E. Związku z tym pole trójkąta AFE nie można jednoznacznie wyznaczyć

kochanus_niepospolitus: chyba że pole tegoż trójkąta pozostawimy jako funkcję zmiennej 'x' (odległość |DF| ).

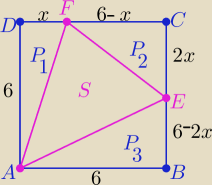
Eta: x∊(0,3) P₁= 3x , P₂= x(6−x)= 6x−x² , P₃=3(6−2x)= 18−6x S= P□ −(P₁+P₂+P₃) ⇒ S(x)=36−(3x+6x−x²+18−6x) ⇒ S(x)=x²−3x+18 −−−−−f. kwadratowa ( parabola ramionami do góry

	3
zatem osiąga minimum dla odciętej wierzchołka xw=		= 1,5
	2

dla |DF|=x= 1,5 −−− ple trójkąta AEF jest najmniejsze

kochanus_niepospolitus: ach ... nie doczytałem treści zadania