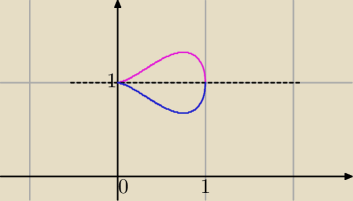
 (y − 1)2 = x2*(x−x2)
(y−1)2≥0⇒x−x2≥0⇔x∊<0,1>
y−1=x*√x−x2 lub y−1=−x*√x−x2
y=1+x*√x−x2 lub y=1−x*√x−x2
Teraz kombinuj.
Masz odpowiedź?
(y − 1)2 = x2*(x−x2)
(y−1)2≥0⇒x−x2≥0⇔x∊<0,1>
y−1=x*√x−x2 lub y−1=−x*√x−x2
y=1+x*√x−x2 lub y=1−x*√x−x2
Teraz kombinuj.
Masz odpowiedź?
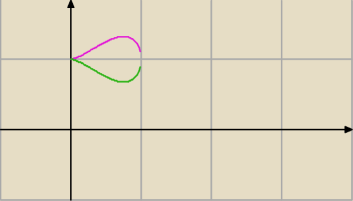 Żeby równanie miało sens musimy założyć, że
x − x2 ≥ 0 ⇒ x(1 − x) ≥ 0 ⇒ x ∊ [0,1]
(y − 1)2 = x3(1 − x) ⇒ y − 1 = ± √x3(1 − x) ⇒ y = ± √x3(1 − x) + 1
y = √x3 − x4 + 1
y = − √x3 − x4 + 1
P = 2 * ∫01(√x3 − x4 + 1)dx
Żeby równanie miało sens musimy założyć, że
x − x2 ≥ 0 ⇒ x(1 − x) ≥ 0 ⇒ x ∊ [0,1]
(y − 1)2 = x3(1 − x) ⇒ y − 1 = ± √x3(1 − x) ⇒ y = ± √x3(1 − x) + 1
y = √x3 − x4 + 1
y = − √x3 − x4 + 1
P = 2 * ∫01(√x3 − x4 + 1)dx
| x | ||
x√x − x2 = x√1/4 − (x − 1/2)2 = | √1 − (2x − 1)2 | |
| 2 |
| t + 1 | ||
2x − 1 = t ⇒ x = | ||
| 2 |
| t + 1 | ||
P = 2 * ∫−11 | √1 − t2dt = | |
| 4 |
| 1 | ||
= | (∫−11t√1 − t2dt + ∫−11√1 − t2dt) | |
| 2 |
| ||||||||
∫−11√1 − t2dt = 2* ∫−10√1 − t2dt = | ||||||||
| 1 | sin2u | π | ||||
= 2 * ∫−π/20{1 + cos2u}{2}du = 2 * ( | u + | )|−π/20 = | ||||
| 2 | 4 | 2 |
| π | ||
P = | ||
| 4 |
