Zadanie maturalne typu wykaż,że... ,
Kleo:
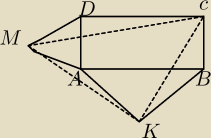
Na dwóch bokach prostokąta ABCD zbudowano trójkąty równoboczne ADM i BAK, jak na rysunku.
Wykaż, że trójkąt MKC (linia przerywana) jest równoboczny.
6 sty 21:54
kochanus_niepospolitus:
Wskazówka:
1) Należy zauważyć, że ΔMDC, ΔMAK i ΔCBK są jednakowe.
2) Kąt ∡DCM oznaczamy jako α, wtedy ∡CMD wynosić będzie (30−α) <poniewąż ∡MDC ma miarę 90+60
<−−− uzasadnij dlaczego tak jest >
Skorzystaj z tych dwóch rzeczy aby wyznaczyć miarę kąta ∡MCK i analogicznie np. ∡CKM
I to już zakończy Twój dowód
6 sty 22:03
Janek191:
'
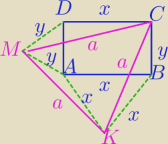
Trójkąty: KCB, KMA, MCD są przystające.
I ∡ B I = I ∡ A I = I ∡ D I = 90
o + 60
o = 150
o
6 sty 22:08
utem:
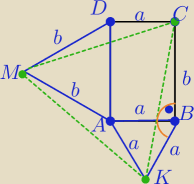
|∡KBC|=90
+60
o=150
|∡KBC|=|∡CDK|=150
o⇔ΔKBC≡ΔCDK cecha bkb
|∡MAK|=360
o−(2*60
o+90
o)=150
o
⇔ΔMAK≡ΔCDK≡ΔKBC
|MK|=|KC|=|MC|
ΔMKC jest trójkątem równobocznym.
6 sty 22:10
 Na dwóch bokach prostokąta ABCD zbudowano trójkąty równoboczne ADM i BAK, jak na rysunku.
Wykaż, że trójkąt MKC (linia przerywana) jest równoboczny.
Na dwóch bokach prostokąta ABCD zbudowano trójkąty równoboczne ADM i BAK, jak na rysunku.
Wykaż, że trójkąt MKC (linia przerywana) jest równoboczny.
 '
Trójkąty: KCB, KMA, MCD są przystające.
I ∡ B I = I ∡ A I = I ∡ D I = 90o + 60o = 150o
'
Trójkąty: KCB, KMA, MCD są przystające.
I ∡ B I = I ∡ A I = I ∡ D I = 90o + 60o = 150o
 |∡KBC|=90+60o=150
|∡KBC|=|∡CDK|=150o⇔ΔKBC≡ΔCDK cecha bkb
|∡MAK|=360o−(2*60o+90o)=150o
⇔ΔMAK≡ΔCDK≡ΔKBC
|MK|=|KC|=|MC|
ΔMKC jest trójkątem równobocznym.
|∡KBC|=90+60o=150
|∡KBC|=|∡CDK|=150o⇔ΔKBC≡ΔCDK cecha bkb
|∡MAK|=360o−(2*60o+90o)=150o
⇔ΔMAK≡ΔCDK≡ΔKBC
|MK|=|KC|=|MC|
ΔMKC jest trójkątem równobocznym.