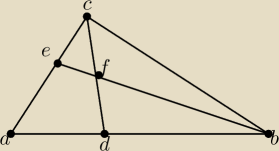
 W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD| : |DB|=1:2 oraz
|AE| : |EC|=1:2. Wyznacz jaką część pola trójkąta ABC stanowi pole czworokąta ADFE.
Będę wdzięczna za każdą pomoc.
W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD| : |DB|=1:2 oraz
|AE| : |EC|=1:2. Wyznacz jaką część pola trójkąta ABC stanowi pole czworokąta ADFE.
Będę wdzięczna za każdą pomoc.
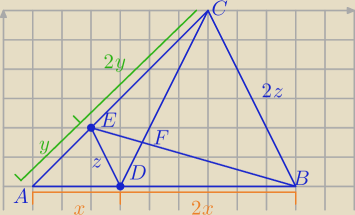 Ozn. PABC = P
Ozn. PABC = P
| 1 | ||
PADE = | P | |
| 9 |
| 1 | ||
PBCD = P{ADC} ⇒ P = 2 * PACD = 2 * ( | P + PEDC ) | |
| 9 |
| 1 | 1 | 7 | ||||
Stąd wyliczmy PEDC = | P − | P = | P | |||
| 2 | 9 | 18 |
| 1 | 7 | 1 | 1 | |||||
= | P + | P + 3PEDF ⇒ 3PEDF = | P ⇒ PEDF = | P | ||||
| 9 | 9 | 9 | 27 |
| 4 | ||
PADFE = PADE + PDFE = | P | |
| 27 |