rownanie kwadratowe, parametr Hebek: Zbadaj liczbę rozwiązań w zależności od wartości parametru k 6x² − 12[x]= k² +3k −4 Mam problem z tym wyznaczeniem liczby rozwiązań, mógłby ktos pomóc? undefined

Godzio: [x] to wartość bezwzględna czy część całkowita?

Hebek: wartosc bezwzgledna

Godzio: Umiesz narysować wykres f(x) = 6x² − 12|x|?

Hebek: Narysowałem tylko problem pojawia sie kiedy mam wyznaczyć liczbe rozwiązan

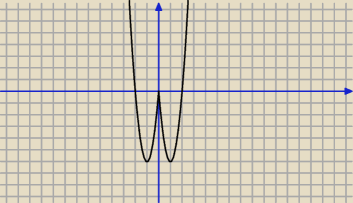
Godzio: Dla k² + 3k − 4 < 6 brak rozwiązań Dla k² + 3k − 4 = 6 oraz k² + 3k − 4 > 0 dwa rozwiązania Dla 6 < k² + 3k − 4 < 0 cztery rozwiązania Dla k² + 3k − 4 = 0 trzy rozwiązania Z każdego warunku trzeba wyliczyć k.

Hebek: Wielkie dzięki Upewniam się, tam gdzie jest 6 to chodziło Ci o −6 tak?

Godzio: Tak tak

PW: Zbadajmy, czy liczba 0 jest rozwiązaniem. Musiałoby być k² + 3k − 4 = 0, (k+4)(k−1)= 0 a to jest możliwe, gdy parametr k osiąga wartość − 4 lub 1. Mamy więc odpowiedź: dla k = − 4 i dla k=1 rozwiązaniem równania jest liczba 0. Należy też zauważyć, że równanie ma wtedy postać 6x² − 12|x| = 0 6|x|² − 12 |x| = 0 6|x|(|x| − 2) = 0, zatem rozwiązaniami oprócz x₀ = 0 są również x₁ = −2 i x₂ = 2. Podsumowanie: dla k = − 4 i dla k = 1 badane równanie ma trzy rozwiązania. Jeżeli x₀ = 0 nie jest rozwiązaniem, czyli prawa strona badanego równania nie jest zerem, to widać, że z parzystości funkcji po lewej stronie wynika, że równanie ma parzystą liczbę rozwiązań − jeżeli jakaś liczba dodatnia x₃ jest rozwiązaniem, to również liczba − x₃ jest rozwiązaniem. Wystarczy zatem ustalić liczbę rozwiązań równania (1) 6x² − 12x = k² + 3k − 4, x∊(0,∞), k≠−4, k≠1. Wskazówka do dalszej części. Rysujemy wykres funkcji f(x) = 6x² − 12x, x∊(0,∞) (minimum równe −6) i wyciągamy wniosek: − równanie (1) ma jedno rozwiązanie, gdy k² + 3k − 4 = − 6 lub gdy k² + 3k − 4 > 0 − równanie (1) ma dwa rozwiązania, gdy − 6 < k² + 3k − 4 < 0.

PW: Przepraszam, zanim udłubałem swoje (przegadane) rozwiązanie, pojawiło się lepsze, którego nie widziałem

Godzio: Twoje rozwiązania zawsze są wartościowe