f kwadratowa z parametrem maniek: Jakie muszą być wartości parametru m, aby wykres funkcji o równaniu f(x)=mx²−(3m−1)x+1 przecinał os OX w dwóch różnych miejscach położonych na prawo od prostej o równaniu x=3? Jakie tu dać założenia oprócz: m>0 Δ>0 x1 i x2> 3

Godzio: Δ > 0 a * f(3) > 0 p > 3

maniek: a * f(3) > 0 możesz to jakos wytłumaczyć?

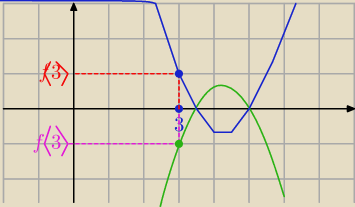
Godzio: Jeżeli a > 0 to f(3) > 0 Jeżeli a < 0 to f(3) < 0 Żeby nie rozpatrywać osobno przypadków możemy hurtem napisać a * f(3) > 0

Godzio: Niebieska parabola się troszkę popsuła ...

maniek: Nie wychodzi mi a gdy wpisałem funkcje w program to rozwiązanie wyszło dla m ok 0.00000009...

maniek: m * f(3)>0 m * [9m − (3m−1)3+1]=m * [9m − 9m + 3 +1]= 4m>0 => m>0

Godzio: A jaka ma być odpowiedź?

Godzio: Mi wychodzi, że takiego m nie ma.

maniek: Właśnie nie mam odpowiedzi do tego zadania.

Godzio: Uzasadnienie, że nie ma takiego m,

	1
x1x2 =
	m

	3m − 1		1
x1 + x2 =		= 3 −		= 3 − x1x2
	m		m

x₁ + x₂ + x₁x₂ = 3 Oba pierwiastki są > 3, a z tego mamy, że tak nie może być.

misiak: oprócz tego warunku trzeba jeszcze ustalić pozycję wierzchołka paraboli na prawo tzn. x_W>3

Godzio: Ten warunek też uwzględniłem przy pierwszej odpowiedzi ( p > 3 )

misiak:

3m−1
	>3
2m

3m−1−6m
	>0
2m

2m(−3m−1)>0 −2m(3m+1)>0

	1
−		<m<0 co jest sprzeczne z pierwszym warunkiem
	3

i potwierdza, że rozwiązania nie ma

Godzio:

misiak: ok już wszystko jasne