Powierzchnia zawarta w walcu ama: Mam za zadanie obliczyć pole części powierzchni z=√x²+y² zawartej we wnętrzu walca x²+y²=2x. Jak to zroibić? Nie chodzi mi nawet o policzenia a o rysunek, bo umiem tylko narysować ten walec, ale to drugie rownanie to już nawet nie wiem gdzie bym miała zmieścić

Godzio: 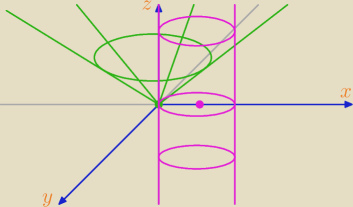z = √x² + y² (x − 1)² + y² = 1

ama: O ja, bardzo dziękuję! A miałabym jeszcze pytanie do tego walca. Myślałam że jego środek znajduje się w początku układu współrzędnych. Czemu więc tak nie jest "normalnie" i jakie muszą być warunki żeby tak było?

Godzio: x² + y² = 2x x² − 2x + y² = 0 x² − 2x + 1 − 1 + y² = 0 (x − 1)² − 1 + y² = 0 (x − 1)² + y² = 1 −− to okrąg o środku w punkcie (1,0) i promieniu 1 Żeby środek był w (0,0) to równanie musiało by być postaci: x² + y² = r²

ama: a, już chyba rozumiem. To wynika z tego, że promień to √2x, więc nie może być wartość ujemna na osi OX tak?

Godzio: Te zielone proste przedstawiają wykresy: W płaszczyźnie OXZ: z = |x| (dla y = 0) W płaszczyźnie OYZ: z = |y| (dla x = 0) A później obkręcamy

ama: Aha, to od tej strony. Bardzo dziękuję za dokładne wytłumaczenie.