długosc okregu i pole koła
kasiula: mam jeszcze takie :
boki prostakata maja długosc 12 i 5 cm .mam obliczyć długosc okregu opisanego na tym
prostokacie.
II− oblicz pole koła wpisanego w kwadrat o przekatnej d=8 cm ( z rysunkiem)
16 gru 16:42
R.W.16l:
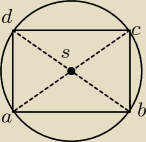
s jest środkiem tego koła, czyli r tego koła jest równy 1/2 przekątnej, czyli
c
2=a
2+b
2
a=12
b=5
c=13 (po obliczeniach)
czyli r = 6,5 (cm)
16 gru 16:46
R.W.16l:
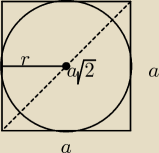
a
√2=8, czyli a=4
√2
r=1/2a=2
√2
Po=8π w takim razie

16 gru 16:48
kasiula: a moze sz mi napisać te obliczenia bo baba mówiłą ze musi byc wszystko plis
16 gru 16:51
kasiula: z góry Ci dziękuje ") jesteś wielki i masz u mnie wielkiego PLUSA thx

16 gru 16:53
R.W.16l: do 1.
s jest środkiem tego koła, czyli r tego koła jest równy 1/2 przekątnej, czyli c
2=a
2+b
2
a=12
b=5
c
2=12
2 + 5
2
c=
√122 + 52
c=
√144+25
c=
√169
c=13
czyli długość przekątnej = 13
| | 13 | |
r=1/2 przekątnej, czyli r= |
| =6,5 (cm) |
| | 2 | |
Dł okręgu to 2πr, czyli Ob=13π
2.
z złotego trójkąta − prostokątny, równoramienny − kąty to: 45:90:45,
przyprostokątne mają długość a,
przeciwprostokątna ma długość a
√2 (a
2+a
2=c
2 ← w tym przypadku b
2, to a
2, czyli 2a
2=c
2,
czyli c=a
√2)
| | 8 | |
jako, że a√2=8, to a= |
| |
| | √2 | |
usuwając niewymierność z pierwiastka:
jako, że kolo wpisane w kwadrat ma promień równy połowie boku a, to r=1/2a, gdzie a to te
4
√2, czyli r=2
√2
Po=πr
2,
podstawiamy
Po=π(2
√2)
2=4
√4=8π
16 gru 17:05
 s jest środkiem tego koła, czyli r tego koła jest równy 1/2 przekątnej, czyli
c2=a2+b2
a=12
b=5
c=13 (po obliczeniach)
czyli r = 6,5 (cm)
s jest środkiem tego koła, czyli r tego koła jest równy 1/2 przekątnej, czyli
c2=a2+b2
a=12
b=5
c=13 (po obliczeniach)
czyli r = 6,5 (cm)
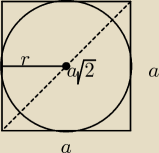 a√2=8, czyli a=4√2
r=1/2a=2√2
Po=8π w takim razie
a√2=8, czyli a=4√2
r=1/2a=2√2
Po=8π w takim razie 
