Zadanie ze stereometrii robdbwa: W ostrosłupie prawidłowym czworokątnym, dana jest zależność pomiędzy długością krawędzi podstawy a długością krawędzi bocznej. b = 3a. Wyznacz miarę konta pomiędzy sąsiednimi ścianami bocznymi. Odp. α = pi − arccos 1/35 Jak do tego podejść?

Eta:

	a2		a
h=√9a2−		=		√35
	4		2

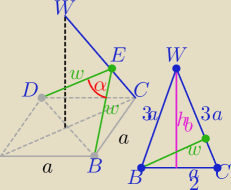
	a*h		a2		3a*w
P(BCW)=		=		√35 i P(BCW)=
	2		4		2

	a√35		35a2
to 6aw=a2√35 ⇒ w=		to w2=
	6		36

i |DB|=a√2 to |DB|²= 2a² Z tw. kosinusów w ΔDBE :

	2w2−|BD|2		a2
cosα=		⇒ cosα= 1−
	2w2		w2

...................

	36		1
cosα= 1−		⇒ cosα= −		i α∊( 0,π)
	35		35

to α= π − arccos1/35

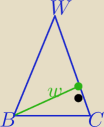
Eta: Zapomniałam zaznaczyć na rys. kąt prosty ( bo w jest też wysokością ΔBCW