pole ograniczone krzywymi malbor:

	1
Obliczyć pole ograniczone: y=		, y=0, x=1
	x2(x+1)

I mam pytanie dlaczego liczymy tylko pole od 0 do 1? Próbowałem to rozbić na trzy pola: P1 od −1 do −1/2 P2 od −1/2 do 0 P3 od 0 do 1 ale widzę, że wychodzi mi źle. Patrze jednak na wykres http://www.wolframalpha.com/input/?i=plot+y%3D1%2F%28x%5E2%28x%2B1%29%29+from+-2+to+2 i nie wiem dlaczego część od −1 do 0 wypada i dlaczego tam nie liczymy pola.

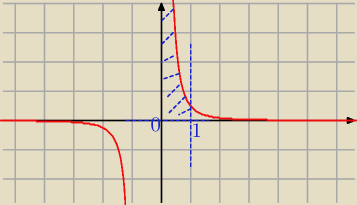
Janek191: y = 0 x = 1

malbor: Ale od −1 do 0 wykres tez jest nad osią OX więc też powinien się do pola liczyć

malbor:

malbor:

kochanus_niepospolitus: źle zaznaczył janek obszar ... całkujesz od x=−1 to x=1

malbor: Tak, a wtedy to pole od −1 wychodzi −∞ i nie wiem czy tak powinno być. Nie bierzemy go po prostu pod uwagę czy jak?

Arturek_lat_7: Bzdura. W x=−1 funkcka ta ma asymptote (nie przyjmuje wartoscicdla x=−1. Dlatego liczy sie granice calki.

piotr1973: Całka w granicy od −1 do 1 jest rozbieżna (nieskończone pole)

malbor: Arturek, wiem ze tam jest asymptota, ale to nie znaczy ze od −1 do 1 nie moge liczyc pola, prawda? piotr, w odpowiedziach mam 1−ln2, ale wolfram rzeczywiście nie oblicza pola http://www.wolframalpha.com/input/?i=area+between+y%3D1%2F%28x%5E2%28x%2B1%29%29%2C+y%3D0%2C+x%3D0 Bardziej wiarygodny wydaje mi się wolfram