| 1 | ||
x≠1 x≠ | ||
| 2 |
| 1 | ||
więc rozwiązaniem są N+ (dodatnie) − {1, | } | |
| 2 |
 bo jeśli wynik mnożenia ma być większy od zera, to żaden nawias nie może być zerowy, bądź
minusowy
−4x2>−9
bo jeśli wynik mnożenia ma być większy od zera, to żaden nawias nie może być zerowy, bądź
minusowy
−4x2>−9
| 9 | ||
x<√ | ||
| 4 |

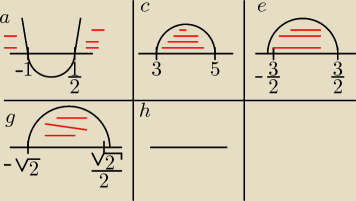 a)
(x+1)(2x−1) > 0
znajdujemy miejsca zerowe (rys) funkcja jest rosnąca
a)
(x+1)(2x−1) > 0
znajdujemy miejsca zerowe (rys) funkcja jest rosnąca
| 1 | ||
x∊(−∞,−1) ∪ ( | ,∞)
| |
| 2 |
| 3 | 3 | |||
x∊(− | , | )
| ||
| 2 | 2 |
| √2 | ||
x∊(−√2, | )
| |
| 2 |

 a)
(x+1)(2x−1) > 0
znajdujemy miejsca zerowe (rys) funkcja jest rosnąca
a)
(x+1)(2x−1) > 0
znajdujemy miejsca zerowe (rys) funkcja jest rosnąca
| 1 | ||
x∊(−∞,−1) ∪ ( | ,∞)
| |
| 2 |
| 3 | 3 | |||
x∊(− | , | )
| ||
| 2 | 2 |
| √2 | ||
x∊(−√2, | )
| |
| 2 |

 robiąc tak jak ty:
9−4x2>0
−4x2>−9
4x2<9
robiąc tak jak ty:
9−4x2>0
−4x2>−9
4x2<9
| 9 | ||
x2< | /√
| |
| 4 |
| 9 | ||
|x| < √ | ||
| 4 |
| 9 | 9 | |||
x<√ | v x>−√ | |||
| 4 | 4 |
| 3 | 3 | |||
x< | v x> − |  i wtedy i wtedy | ||
| 2 | 2 |
 sorki
sorki
 1.Rozwiąż nierówności:
a) x(1−3x) < 0
b) 4x²≤5x
c)x > 6x²
d) (−x+5)(x+2)>0
e)(1+x)(3−2x)≤0
f) − √3x² + 3x <0
g)x²<1
h) ⅓ x ²+4>0
i) −2x² ≥0
j) x² ≥4
k)−4x²−1<0
l) x²+8 ≥0
m) x²<2−x
n) x−7≥5x²
o)4x²+49≤28x
p)3x²+7≥5x
r)4x²≥4x−1
s)9x²+12x+4>0
t)9+25x²≤30x
u)8x−1>16x²
w)−x²+2x−5>0
x)2x²−3x+4≥0
y)(2x−1)²>16
z)(3x+1)²+3<0
1.Rozwiąż nierówności:
a) x(1−3x) < 0
b) 4x²≤5x
c)x > 6x²
d) (−x+5)(x+2)>0
e)(1+x)(3−2x)≤0
f) − √3x² + 3x <0
g)x²<1
h) ⅓ x ²+4>0
i) −2x² ≥0
j) x² ≥4
k)−4x²−1<0
l) x²+8 ≥0
m) x²<2−x
n) x−7≥5x²
o)4x²+49≤28x
p)3x²+7≥5x
r)4x²≥4x−1
s)9x²+12x+4>0
t)9+25x²≤30x
u)8x−1>16x²
w)−x²+2x−5>0
x)2x²−3x+4≥0
y)(2x−1)²>16
z)(3x+1)²+3<0