Badania przebiegu zmienności funkcji lungi:

	x+1
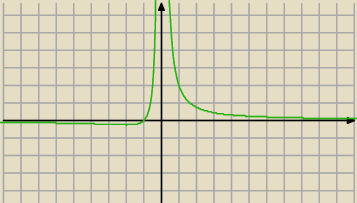
Zbadaj przebieg zmienności i naszkicuj wykres funkcji: f(x)=
	x2

Mam problem z tego typu zadaniami, bo wszystko dobrze idzie przez większość przykładu, dopóki nie trzeba ogarnąć tabelki i na jej podstawie narysować wykresu. Mam wrażenie, że uwzględniam nie to, co trzeba i później wychodzi źle. Mam dziedzinę funkcji: R\{0}, policzyłam granice na końcach i wyszło 0, policzyłam miejsce przecięcia z osią OX: (−1,0)

	−(x+2)
Potem policzyłam pochodną i wyszło tak jak w odp.		, a dziedzina pochodnej R\{0}.
	x3

Dalej chciałam wyznaczyć przedziały monotoniczności, f'(x)=0 i wyszło mi, że f'(x) >0 dla x (−niesk., −2) i f'(x)<0 dla x (−2, +niesk.) Nie wiem czy to jest ok. Natomiast wykres to już jakaś masakra dla mnie. x (−niesk., −2) −2 (−2, −1) −1 (−1,0) 0 (0, +niesk.) f'(x) + 0 − − − X − f(x) rośnie −1/4 maleje maleje maleje maleje Przepraszam, że tak brzydko to wyszło, nie wiem, czy tu jakoś można zrobić tabelki. Podejrzewam, że ta tabelka jest źle i dlatego źle mi wychodzi, nie umiem się do tego zabrać.

Jerzy:

lungi: Okeej, ale chciałabym wiedzieć czemu na wykresie od minus niesk. do 0 ta funkcja rośnie, a od 0 do plus niesk. maleje. Bo z mojej tabelki wychodzi inaczej (chyba?). widzę że tam gdzie jest −1 to powinno być 0 w f'(x), ale dalej nie wiem o co biega. Rozumiem że to miejsce zerowe etc. Ale chcę wiedzieć co u mnie jest nie tak.

lungi: w f(x) *

Jerzy: funkcja ma minimum dla x = −2

lungi: czyli najpierw maleje, potem minimum, potem rośnie. Od 0 do plus niesk. maleje i to mi wychodzi. Czyli w związku z tym przedziały monotoniczności pochodnej mam źle policzone?