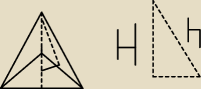
 Podstawą ostrosłupa jest trójkąt prostokątny równoramienny, a wysokość ostrosłupa jest równa
przeciwprostokątnej tego trójkąta. Każda ściana poczna tworzy z podstawą kąt α. Wyznacz tgα.
Przeciwprostokątną oznaczam jako b, przyprostokątne jako a. Wysokość H wynosi również b. Jak z
tego coś wyprowadzić?
Podstawą ostrosłupa jest trójkąt prostokątny równoramienny, a wysokość ostrosłupa jest równa
przeciwprostokątnej tego trójkąta. Każda ściana poczna tworzy z podstawą kąt α. Wyznacz tgα.
Przeciwprostokątną oznaczam jako b, przyprostokątne jako a. Wysokość H wynosi również b. Jak z
tego coś wyprowadzić?

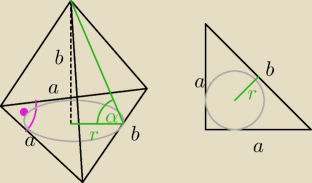
| 1 | a2 | ||
r(2a+b) = | |||
| 2 | 2 |
| a2 | ||
r = | ||
| 2a+b |
| b | ||
tgα = | ||
| r |
| 1 | a2 | |||
ale skąd wiemy, że | r(2a+b)= |  | ||
| 2 | 2 |
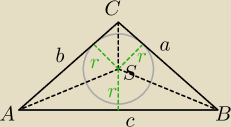 Jest taki wzór
S = poleΔABC = poleΔASB + poleΔBSC + poleΔCSA = 12c*r + 12a*r + 12b*r =
= 12r(a+b+c)
gdy a = b
Jest taki wzór
S = poleΔABC = poleΔASB + poleΔBSC + poleΔCSA = 12c*r + 12a*r + 12b*r =
= 12r(a+b+c)
gdy a = b
| a2 | 1 | |||
S = | = | r(2a+c) | ||
| 2 | 2 |
