Okrąg i styczność
Metis:
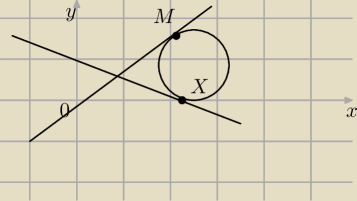
Mam okrag który jest styczny do dwóch prostych których równania znam , znam także jeden punkt
styczności jedną z prostych M.
Jak obliczyć punkt stycznosci z drugą prostą X ?
Nie znając promienia i środka.
6 sty 12:14
Metis: Układałem układy równan ale nic nie wychodziło sensownego
6 sty 12:15
5-latek:
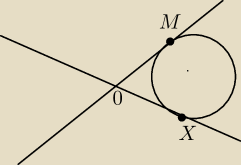
Czesc .
Może wykorzystaj to ze OM=OX
6 sty 12:18
Metis: O to może być pomysł!

Dzięki
5−latku w układzie wsp nie zauwazyłem tego.
6 sty 12:21
Metis: Jednak nie wyliczę z tego wsp. punktu

6 sty 14:42
olekturbo: Podaj całe zadanie.

6 sty 14:43
Kacper:
Masz równanie okręgu okręgu i równania prostych?
Jeśli tak, to układ równań i wyznaczasz punkty styczności.
6 sty 14:44
Metis: Nie mam równania okregu.
Wiem że zawiera się miedzy dwiema prostymi gdzie jeden punkt stycznosci jest podany
6 sty 14:46
henrys: będą dwa takie punkty
punkt przecięcia prostych jest środkiem odcinka o długości 2|OM|, na prostej X wyznaczasz końce
tego odcinka
6 sty 14:49
Metis: Henrys to układ współrzednych, mało widoczny.
6 sty 14:51
henrys: pomyśl jeszcze raz

Jeśli masz dane równania prostych to wyznaczysz ich punkt przecięcia. Współrzędne punktu
styczności pozwolą ci wyznaczyć długość odcinka OM.
6 sty 14:53
Metis: Tak, współrzędne ich punktu wspólnego od razu znalazłem

Rozwiązując układ równań.
Wyznaczyłem długość odcinka OM i ma on 10
√2.
Mam też punkt zaczepienia, bedacy punktem przeciecia prostych, ale nie obliczę z tego
współrzędnych. Czegoś brakuje.
6 sty 14:56
henrys: wszystko jest, ten punkt przecięcia jest środkiem odcinka PP', gdzie P, P' to szukane punkty,
leżące na drugiej prostej
6 sty 14:58
henrys: inaczej szukasz punktów leżących na drugiej prostej oddalonych od punktu O o 10√2
6 sty 14:59
Metis: Zaraz to przeliczę.
Dzięki

6 sty 15:00
piotr: rozwiąż układ równań:
(x−xo)2+(y−yo)2=|OM|2
y=ax+b − równanie prostej nie zawierającej punktu M
Będą dwa rozwiązania, a więc dwa możliwe okręgi styczne
6 sty 15:17
Metis:
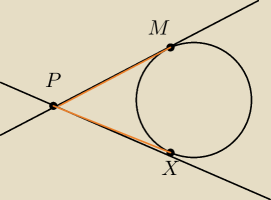
Nadal wydaje mi się, że nic nie zrobię.
X=(x
1,y
1)
M=(2,1)
P=(−12,−1)
|PM|=|PX|=10
√2
Z środka obliczę tylko M'.
6 sty 15:17
Kacper:
A zrobiłeś to, o co cię wszyscy prosili? Dostaniesz dwa punkty i jeden z nich jest szukanym
punktem X.
6 sty 15:19
Metis: Nie widzę tego.
6 sty 15:28
Metis: Wiem ze P jest srdokiem XX' ale nie wyliczę z tego zadnych współrzednych.
Wiem też ze długość XX'=20√2 ale z tego też niczego nie wydobędę.
6 sty 15:31
Metis: Okey juz wiem jak to zrobić.
Wykreśle okrąg o r= |PX|
Srodek to P.
Uzyskam dwa punkty X i X'.
Podobnie jak piotr
6 sty 15:38
utem:
Może napisz całe zadanie, czasem wszystko jest proste przy niektórych danych.
6 sty 15:40
Metis: Proszę
Milu 
Oblicz promień mniejszego z dwóch okręgów stycznych w punkcie M=(2,1) do prostej x−7y+5=0 i
jednoczeście stycznych do prostej x+y+13=0
6 sty 15:44
henrys: ech, Metis, Ty przecież sobie całkiem nieźle radzisz...
O=(a,b) masz
Ax+By+C=0 masz
|OX|2 masz X=(x,y)
|OX|2=(x−a)2+(y−b)2
układ równań (x−a)2+(y−b)2=|OX|2
Ax+By+C=0
wstaw co znasz i rozwiąż
6 sty 15:44
Metis: Wpadłem w zły tok myślenia
Henrys 
6 sty 15:50
utem:
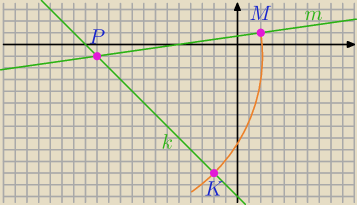
m: x−7y+5=0
k: x+y+13=0
P=(−12,−1)
M=(2,1)
|PM|
2=200
(x+12)
2+(y+1)
2=200
x+y+13=0
−−−−−−−−−−−
x=−22 i y=9
lub
x=−2 i y =−11 wybieramy punkt dla którego y<0
K=(−2,9)
Możesz znaleźć środek okręgu wpisanego w kąt MPK, a potem promień.
6 sty 16:08
Metis: Dziękuje
Milu 
Przy okazji jak formalnie uzasadnić, że wybieram akurat ten okrąg. W koncu proszą o promień
mniejszego . Z rysunku jest to jasne, a jak to ładnie zapisać?

6 sty 16:13
utem:
Wybierasz okrąg w kącie ostrym.
6 sty 16:28
utem:
Pisz następne zadanie. Z jakiego to zbioru?
6 sty 16:29
Metis: To zadanie pochodziło z II| etapu Diamentu 13/14.
Rozwiązuje je + zadania z korespondencyjnego kursu matematyki z Wrocławia.
Próbuję zrobić jak najwięcej przed II etapem

6 sty 16:33
utem:
Powodzenia.

6 sty 16:43
Metis: (Nie) dziękuje

6 sty 16:44
utem:
Oblicz promień mniejszego z dwóch okręgów stycznych w punkcie M=(2,1)
do prostej x−7y+5=0 i jednocześnie stycznych do prostej x+y+13=0.
Inny sposób.
Wektory. Korzystam z rysunku 16: 08.
m: x−7y+5=0
k: x+y+13=0 wektor normalny prostej: u→=[1,1] wektor kierunkowy k1→=[1,−1]
lub k2→=[−1,1]
P=(−12,−1), M=(2,1)
PM→=[14,2]
|PM|2=200
PK→=m*[1,−1]=[m,−m] i |PK|=√200
Wybieram wektor kierunkowy [1,−1] ponieważ punkt K leży na prawo od punktu P.
| [m,−m] |=√200⇔m2+m2=200, m>0
m2=100
m=10
PK→=[10,−10]
P=(−12,−1)→T[10,−10]→K=(−12+10, −1−10)=(−2,−11)
K=(−2,−11)
=======
7 sty 17:04
Metis: 
7 sty 18:28
 Mam okrag który jest styczny do dwóch prostych których równania znam , znam także jeden punkt
styczności jedną z prostych M.
Jak obliczyć punkt stycznosci z drugą prostą X ?
Nie znając promienia i środka.
Mam okrag który jest styczny do dwóch prostych których równania znam , znam także jeden punkt
styczności jedną z prostych M.
Jak obliczyć punkt stycznosci z drugą prostą X ?
Nie znając promienia i środka.
 Czesc .
Może wykorzystaj to ze OM=OX
Czesc .
Może wykorzystaj to ze OM=OX
 Dzięki 5−latku w układzie wsp nie zauwazyłem tego.
Dzięki 5−latku w układzie wsp nie zauwazyłem tego.


 Jeśli masz dane równania prostych to wyznaczysz ich punkt przecięcia. Współrzędne punktu
styczności pozwolą ci wyznaczyć długość odcinka OM.
Jeśli masz dane równania prostych to wyznaczysz ich punkt przecięcia. Współrzędne punktu
styczności pozwolą ci wyznaczyć długość odcinka OM.
 Rozwiązując układ równań.
Wyznaczyłem długość odcinka OM i ma on 10√2.
Mam też punkt zaczepienia, bedacy punktem przeciecia prostych, ale nie obliczę z tego
współrzędnych. Czegoś brakuje.
Rozwiązując układ równań.
Wyznaczyłem długość odcinka OM i ma on 10√2.
Mam też punkt zaczepienia, bedacy punktem przeciecia prostych, ale nie obliczę z tego
współrzędnych. Czegoś brakuje.

 Nadal wydaje mi się, że nic nie zrobię.
X=(x1,y1)
M=(2,1)
P=(−12,−1)
|PM|=|PX|=10√2
Z środka obliczę tylko M'.
Nadal wydaje mi się, że nic nie zrobię.
X=(x1,y1)
M=(2,1)
P=(−12,−1)
|PM|=|PX|=10√2
Z środka obliczę tylko M'.
 Oblicz promień mniejszego z dwóch okręgów stycznych w punkcie M=(2,1) do prostej x−7y+5=0 i
jednoczeście stycznych do prostej x+y+13=0
Oblicz promień mniejszego z dwóch okręgów stycznych w punkcie M=(2,1) do prostej x−7y+5=0 i
jednoczeście stycznych do prostej x+y+13=0

 m: x−7y+5=0
k: x+y+13=0
P=(−12,−1)
M=(2,1)
|PM|2=200
(x+12)2+(y+1)2=200
x+y+13=0
−−−−−−−−−−−
x=−22 i y=9
lub
x=−2 i y =−11 wybieramy punkt dla którego y<0
K=(−2,9)
Możesz znaleźć środek okręgu wpisanego w kąt MPK, a potem promień.
m: x−7y+5=0
k: x+y+13=0
P=(−12,−1)
M=(2,1)
|PM|2=200
(x+12)2+(y+1)2=200
x+y+13=0
−−−−−−−−−−−
x=−22 i y=9
lub
x=−2 i y =−11 wybieramy punkt dla którego y<0
K=(−2,9)
Możesz znaleźć środek okręgu wpisanego w kąt MPK, a potem promień.
 Przy okazji jak formalnie uzasadnić, że wybieram akurat ten okrąg. W koncu proszą o promień
mniejszego . Z rysunku jest to jasne, a jak to ładnie zapisać?
Przy okazji jak formalnie uzasadnić, że wybieram akurat ten okrąg. W koncu proszą o promień
mniejszego . Z rysunku jest to jasne, a jak to ładnie zapisać? 



